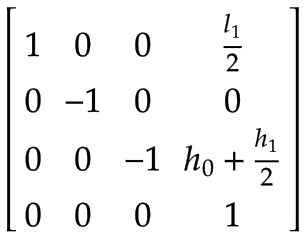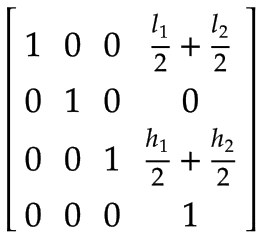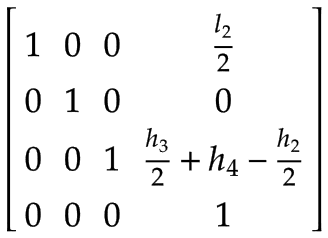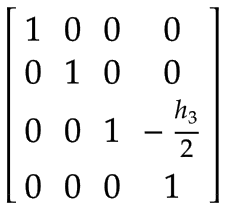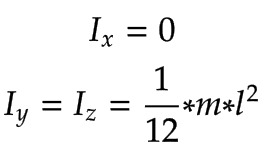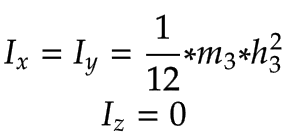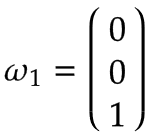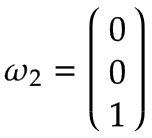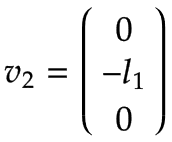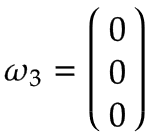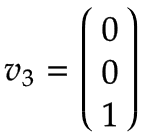動的ロボットモデル

を参照してください Robotics_DynamicModel.project のインストールディレクトリにあるサンプルプロジェクト CODESYS 下 ..\CODESYS SoftMotion\Examples.

移動中の軸のトルク/力を制限するには、現在の軸の状態 (位置、速度、および加速度) からこれらの値を計算する動的モデルが必要です。この例には、次の部分が含まれています。

パート 1 では、既存の動的モデルをアプリケーションで使用する方法と、いくつかのサンプル動作の結果を示します。
パート 2 では、KM Lynch と FC Park の共著「Modern Robotics」に記載されているアルゴリズムに基づいて、SCARA ロボットの動的モデルを作成する方法を説明します。

アプリケーションの構造

パート 1: アプリケーションでの動的モデルの使用

この部分のコードは、 TorqueLimitationDemoフォルダ。
PLC_PRG テスト動作をトリガーするステートマシンを含むメインプログラムです。
動きは、 Trace。

パート 2: 動的ロボットモデルの作成

動的モデルのコードは、 DynModel フォルダ。
DynModel_Scara2_Z SCARAロボットの動的モデルです。
DynModel_Tests すべてのテストを実行します Test_DynModel_Scara2_Z よくある間違いをチェックします。

動的モデルは、2 つの回転ジョイントと 1 つの直動 Z 軸を持つスカラロボットに基づいています。動的モデルに必要な寸法と座標系を備えたロボットの図を以下に示します。

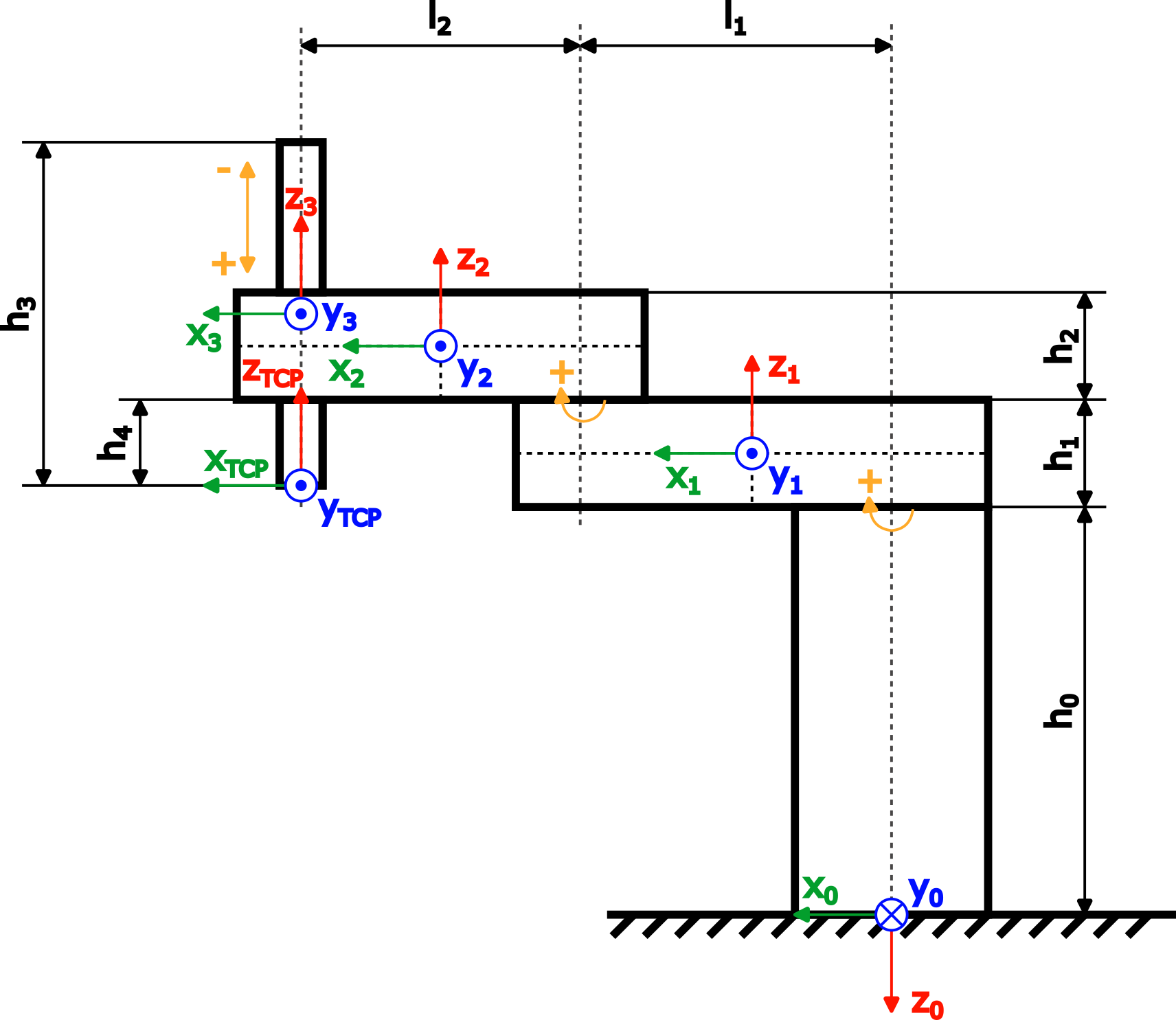
図の寸法	関数ブロック DynModel_Scara2_Z のサンプルプロジェクトの対応する変数名
`h0`	`baseHeight`
`h1`	`armOneHeight`
`h2`	`armTwoHeight`
`h3`	`zAxisLength`
`h4`	`zAxisOffset`
`l1`	`armOneLength`
`l1`	`armTwoLength`

パート 1: アプリケーションでの動的モデルの使用

アプリケーションで動的モデルを使用するには、 ISMDynamics のインターフェース SM3_Dynamics 図書館。からの動的モデルパート 2: 動的ロボットモデルの作成がこのデモンストレーションに使用されます。

モデルは、次を使用して軸グループに割り当てることができます SMC_GroupSetDynamics.この手順では、MCS に対する重力加速度を設定する必要があります。この例のスカラは床に取り付けられているため、重力加速度は正の z0 方向を指します。重力加速度は、ユーザー単位 u/s² で指定する必要があります。この例のすべての長さはユーザー単位 m で定義されているため、重力加速度も m/s² で指定する必要があります。

SMC_ChangeDynamicLimits 各軸の制限を調整するために使用できます。を使用して、軸グループを再度有効にする必要があることに注意してください。 MC_GroupEnable 新しい動的制限をアクティブにするため。

追加の質量が TCP に追加される場合 (たとえば、ロボットによってピックアップされるツールまたはオブジェクト)、 SMC_GroupSetLoad 負荷の定義に使用できます。

の PLC_PRG プログラムには上記のすべてのコンポーネントが含まれており、2 つのテスト動作を実行します。

動き 1

ムーブメント 2

(a0=0°, a1=0°, a2=0 m) から (a0=90°, a1=0°, a2=0.02 m) までのまっすぐな腕の動き:

(a0=0°, a1=-120°, a2=0 m) から (a0=90°, a1=-120°, a2=0,02 m) への角度付きアームの動き:

各移動は、次の境界条件で 3 回連続して実行されます。

全軸のトルク制限は無限（無制限）です。
アーム 2 のトルク制限は、無制限移動時の最大到達トルクよりも低い値に設定されています。値は任意に設定されました 2 Nm.
アーム 2 のトルク制限はそのままです。 2 Nm、さらに負荷が TCP に適用されました (mLoad=3 kg、 lLoad=0.2 m):

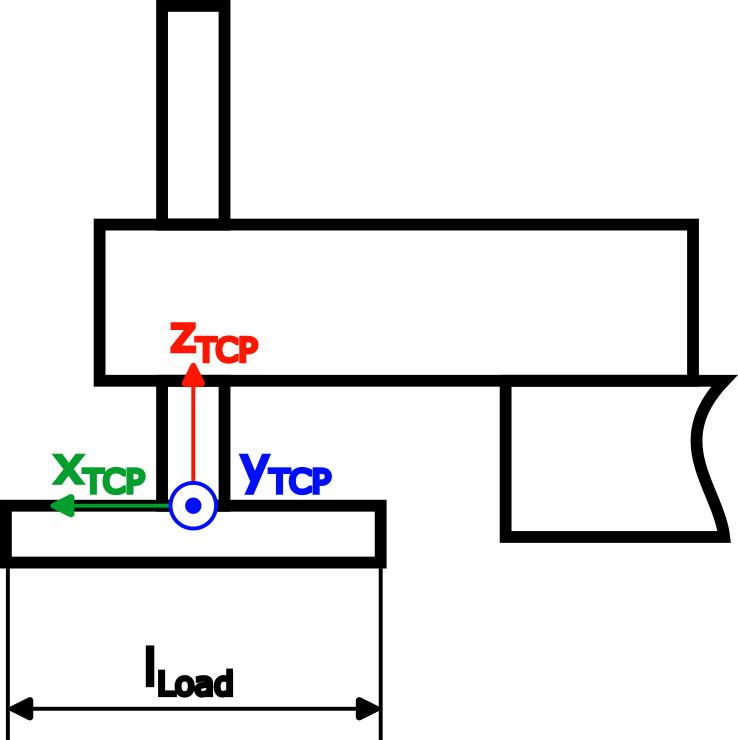負荷の慣性計算は、細いロッドを使用することで簡素化されました。

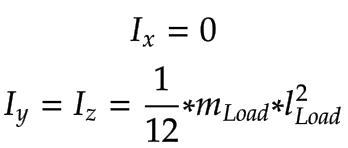動きはトレースで監視できます。移動 1 の結果は次のとおりです。

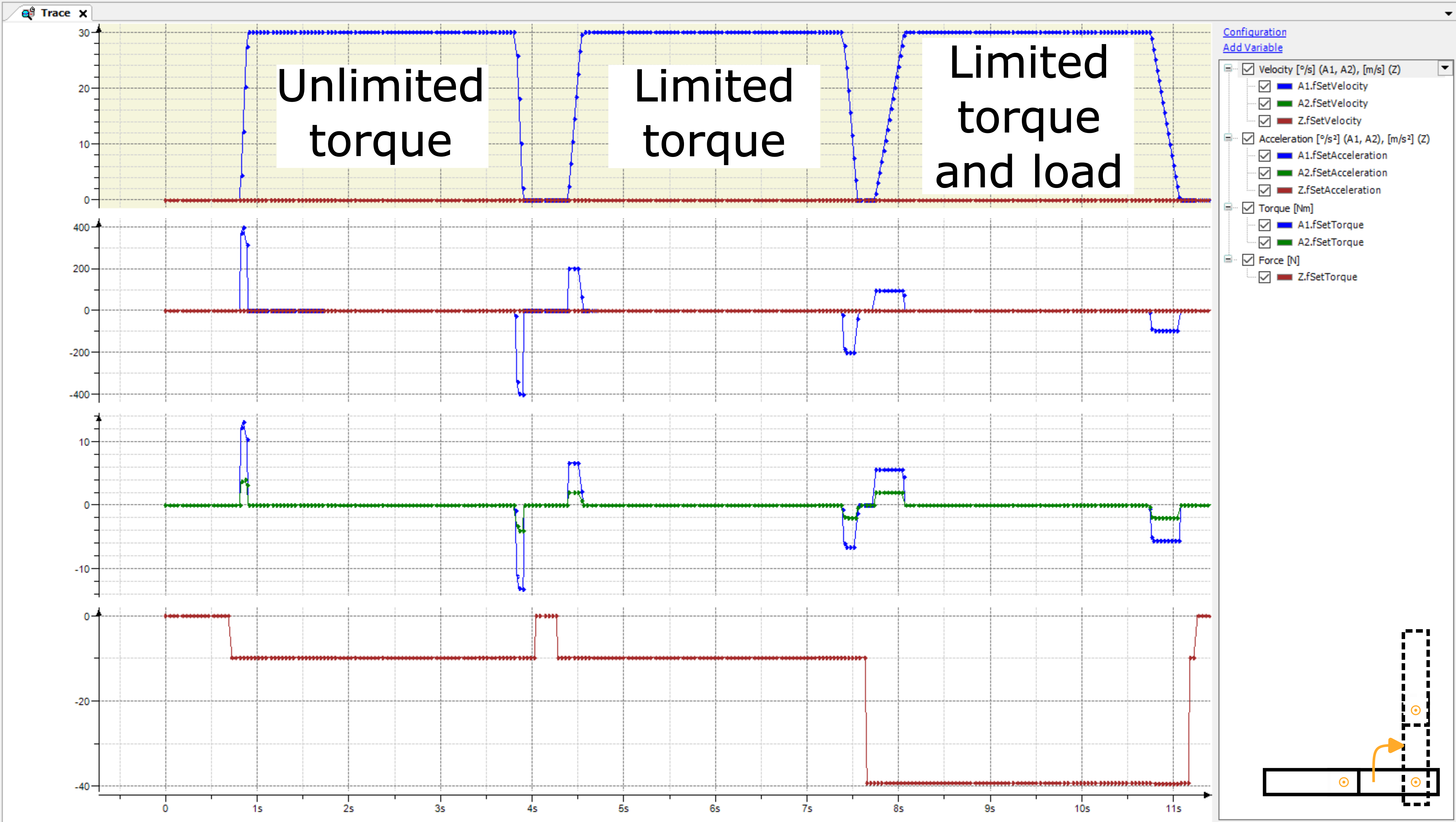
アーム 2 は移動 1 で移動しませんが、アーム 1 の移動により加減速時にアーム 2 にトルクが発生します。計算されたトルクはドライブに送信され、コントローラモードでコントローラループを改善できる可能性があります。 SMC_velocity また SMC_position.トルクフィードフォワード制御ともいう。
トルクを制限した 2 回目の実行では、アーム 2 が動かなくても、アーム 2 のトルク制限によってアーム 1 の動きが遅くなることを示しています。動的モデルがなければ、アーム 1 の加速と減速を手動で減らす必要があります。アーム 2 に過度の機械的ストレスがかかるのを防ぐためです。
負荷のある 3 回目の実行では、アーム 2 のトルク制限に違反しないように、アーム 1 の動きをさらに遅くします。

動的モデルを使用する利点は明らかです。動的モデルを使用せずに過度の機械的応力を防止するには:

ロボットの現在の状態に応じて、すべての動きの動的制限を設定する必要があります。
または、すべての潜在的な動きがどの軸にも過度の機械的ストレスをもたらさないように、すべての軸の動的制限を減らす必要があります。

最初の方法は複雑なタスクであり、妥当な制限を計算するのが難しい場合があります。一方、2 番目の方法では、ほとんどの場合、動きができるだけ速くなりません。これらの欠点は、動的モデルには存在しなくなりました。これは、ロボットが各軸の機械的制限を尊重しながら常に可能な限り速く動くためです。

これらの利点は、動き 2 の結果によって示されます。

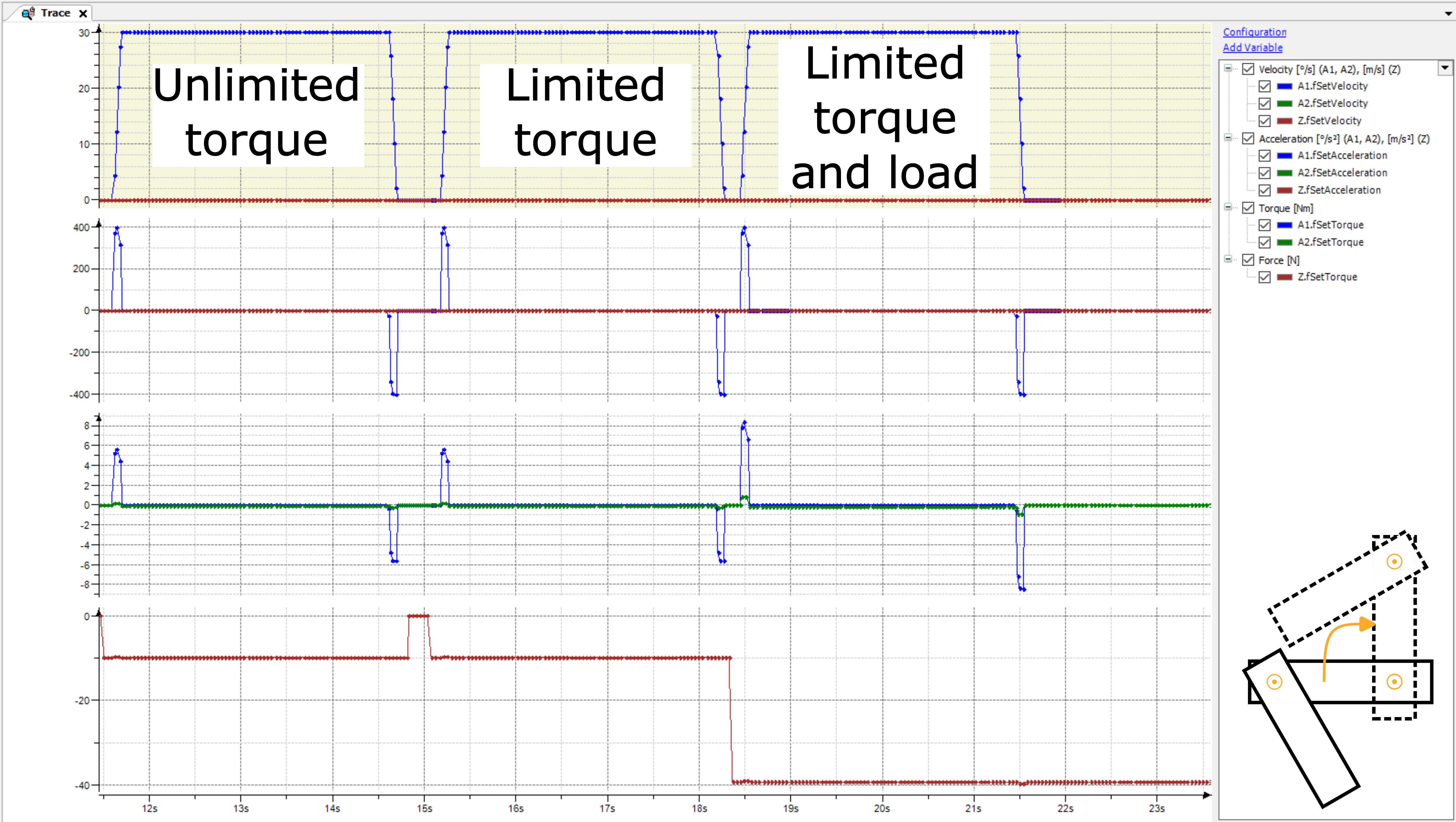
アーム 2 が角度を付けられているため、アーム 2 の結果のトルクは動作 1 よりもかなり低くなります。したがって、3 つの実行すべてが軸トルクによって制限されることはありません。動作 1 に基づいて調整された動的制限を使用した場合 (アーム 2 のトルク制限に違反しないように加速と減速を減らします)、この動作は必要以上に遅くなります。

パート 2: 動的ロボットモデルの作成

この例で作成されたモデルは、KM Lynch と FC Park による書籍「Modern Robotics」で紹介されているオープンチェーンロボットのアルゴリズムに基づいています (第 8 章「Dynamics of Open Chains」を参照)。このアルゴリズムの説明は、この例の範囲を超えています。代わりに、この例では、アルゴリズムの入力値を定義する方法に焦点を当てています。

単純化

この例をより理解しやすくするために、いくつかの簡略化が行われています。

腕の長さ l1 と l2 (回転軸間の距離) は、それぞれの合計アーム長として使用されます。
質量の中心は常に各リンクの幾何学的中心に位置します。
アームと Z 軸の空間慣性行列は、細いロッドに対して計算されます。

動的モデルの要件

SoftMotionアプリケーションでダイナミックモデルを使用するには、このモデルは ISMDynamics インターフェースの SM3_Dynamics 図書館。

動的モデルのゼロ位置、座標系、正の回転方向は、理論的には運動学的モデルから逸脱する可能性があります。ただし、これらの違いを考慮する必要があるため、動的モデルを単純化するために、運動学的モデルの定義を使用することをお勧めします。

動的モデルは Nm 単位のトルク値と N 単位の力を計算する必要があるため、長さのユーザー単位 u を SI 単位 m に変換する必要があります。変換係数は、 SMC_GroupSetUnits に含まれており、 addParams の入力 ISMDynamics.AxesStateToTorque.この例では、長さに m のみを使用しているため、変換係数を無視できます。

モデルの形状データと動的データの仕様

KM Lynch と FC Park による書籍「Modern Robotics」で紹介されているアルゴリズムの IEC 実装 (第 8 章「Dynamics of Open Chains」を参照) には、次の入力値が必要です。

ロボットがホームポジションにあるときの各リンクの重心位置。位置は前のリンクの座標系で指定されます (最初のリンクはベース座標系を基準にして指定されます)。
各リンクの空間慣性マトリックスと質量は、それぞれのリンクフレームで表されます。
ベースフレームで表現された各ジョイントのネジ軸。

重心位置

各リンクの重心位置を示すフレームは次のとおりです。

リンク

フレーム

アーム1

ベース座標系 x で表されるアーム 1 の重心₀、y₀、z₀:

x0 軸を中心に 180° 回転していることに注意してください。

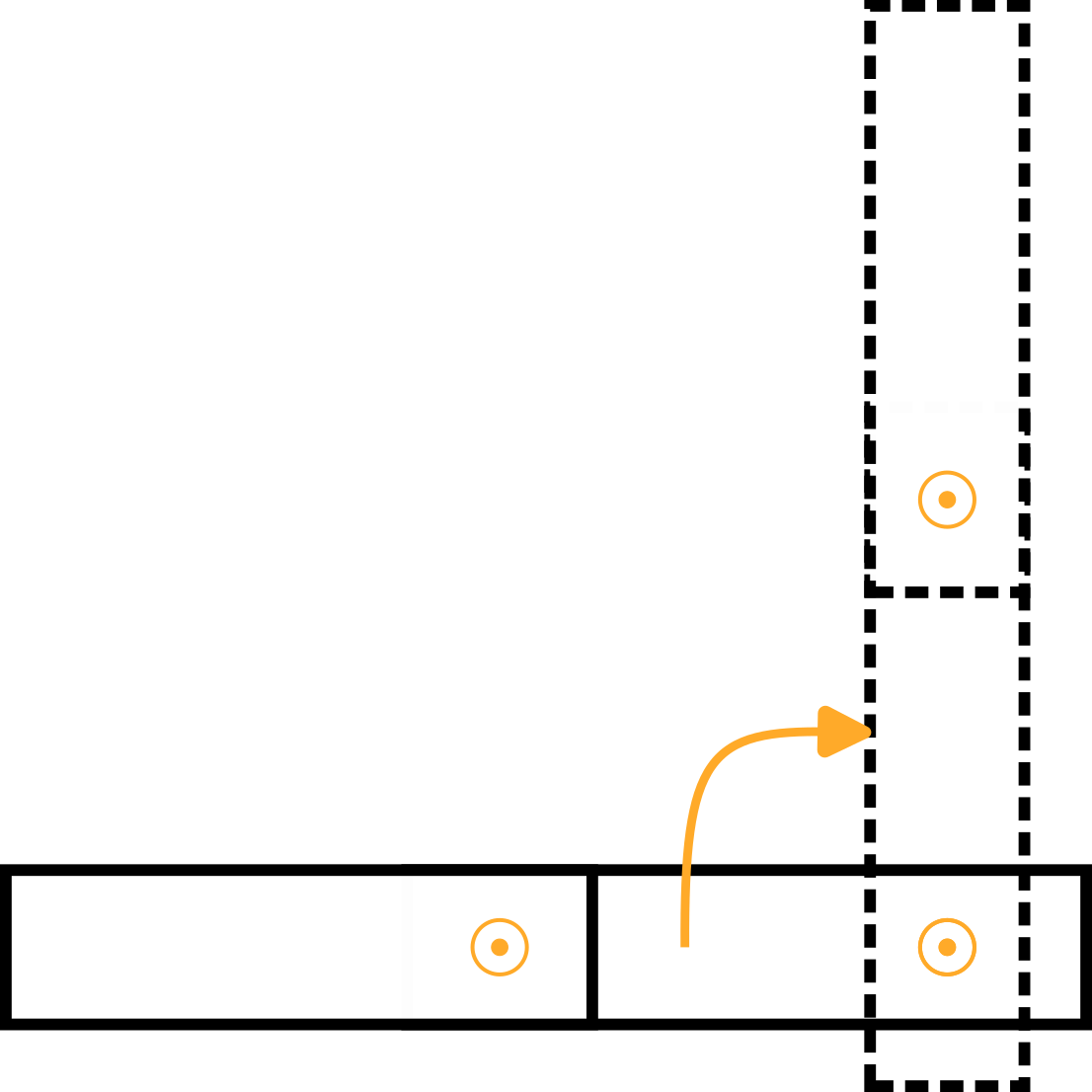
アーム 2

アーム 1 の座標系で表される、アーム 2 の重心:

Z軸

アーム 2 の座標系で表される Z 軸の重心:

工具中心点 (TCP)

Z 軸の座標系で表される、TCP での任意の負荷 (たとえば、ツール、製品、または両方の組み合わせによる) を処理するための 1 つの追加フレーム:

空間慣性行列

空間慣性値は、それぞれのリンクフレームで表現する必要があります。フレームは質量の中心で定義されるため、空間慣性は 3x3 の回転慣性行列と物体の質量で表すことができます。

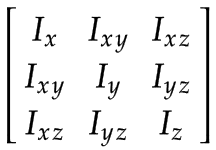ジョイントに細いロッドを使用することを簡略化すると、回転慣性マトリックスの成分は次のようになります。

リンク

空間慣性マトリックス

アーム1、アーム2

対応する質量を持つアーム 1 とアーム 2 m1 と m2、および長さ l1 と l2:

Z軸

ねじ軸

すべてのジョイントのねじ軸は、ベース座標系 x を基準にして表現する必要があります₀、y₀、z₀.

リンク

ねじ軸

アーム1

ターンテーブルがジョイント 1 の周りを正の方向に 1 rad/s の角速度で回転しているとします。

ベース座標系で表される、これは z を中心とした正の回転です。₀-右手の法則に従った軸:

アーム 1 の回転軸はベース座標系の中心に等しいため、直線速度はゼロです。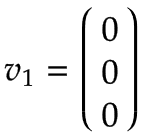

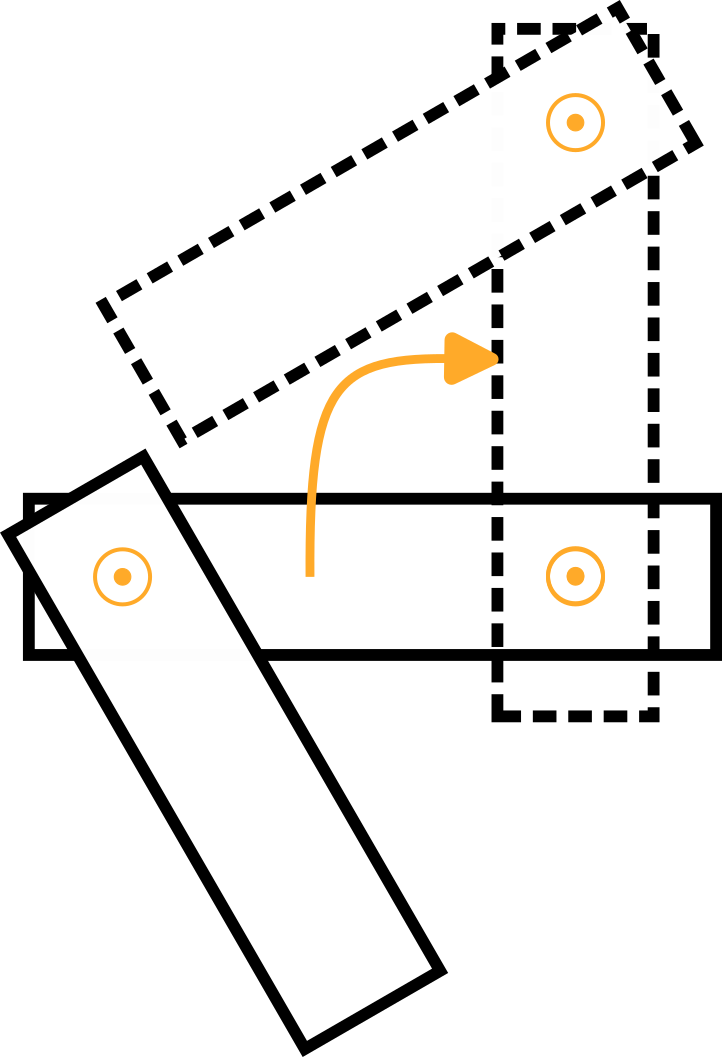
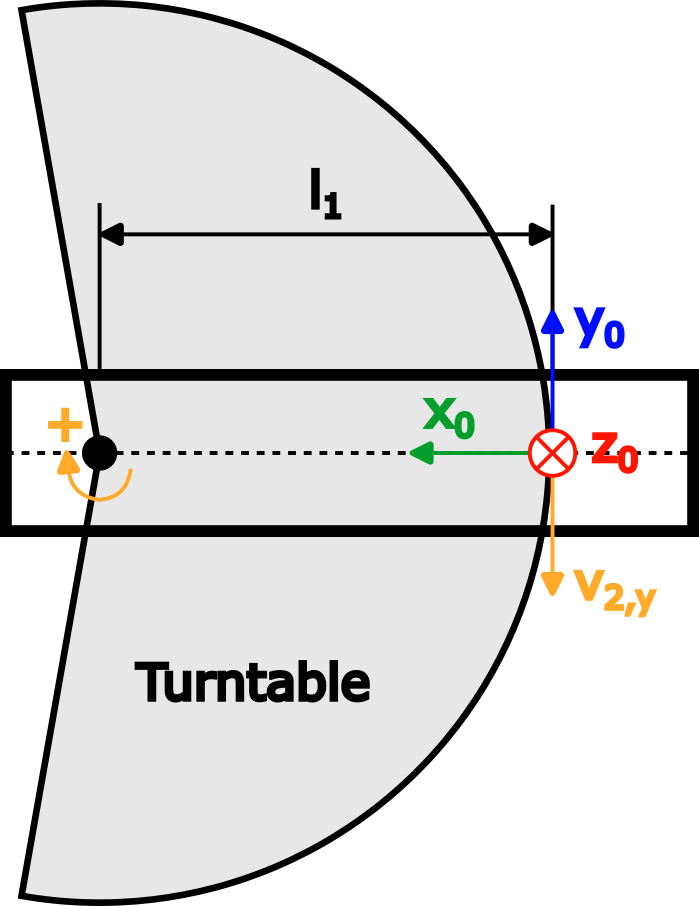
アーム 2

再び、次の図のアーム 1 の上面図に示されているように、1 rad/s の角速度でジョイント 2 の周りを正の方向に回転するターンテーブルを想像してください。

アーム 1 に関しては、角速度は次のとおりです。

図は、結果の線速度 v を示しています。_2,年、これは負の y を指します₀ 方向であり、v に等しい_2,年=-ω_2,z * l₁.

Z軸

Z 軸は、次の規則が適用されるプリズム軸です。

角速度ベクトル ω はゼロです。
直線速度ベクトルは、正の並進方向の単位ベクトルです。

これにより、ベース座標系 x で表される次のベクトルが得られます。₀、y₀、z₀:

テスト

すべてのモデルパラメーターが定義されているため、動的モデルをテストできるようになりました。このセクションには、モデルのいくつかの基本的なテストが含まれています。

ねじ軸の確認

ねじ軸 S 角速度 ω と線速度 v の要素として表現できます。 se(3):

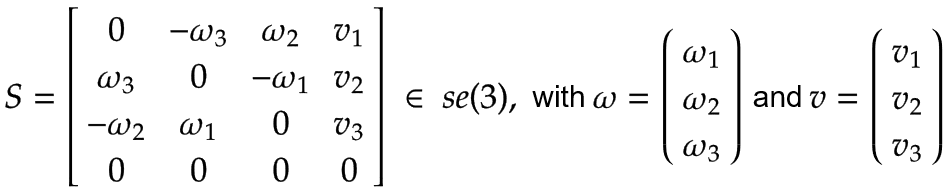前方変換 T ネジ軸で実行可能 S、エンドエフェクタフレーム M ロボットのゼロ位置と関節角度 θ 各関節の:

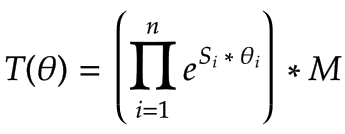サンプルプロジェクトには、この方程式を解く関数が既に含まれています ( SMC_OpenChainKinematics_SolveForward）。詳細については、KM Lynch と FC Park による著書「Modern Robotics」を参照してください。

順変換方程式を使用して、既知の軸位置でテストを実行し、変換が期待される結果につながるかどうかを確認できるようになりました。

停止時のトルク計算の確認

質量中心の位置フレームを確認するには、特定の軸位置で停止時の軸トルクを手動で計算し、モデルによって計算された値と比較します。この例は床に取り付けられた SCARA ロボットに基づいているため、停止時のすべての軸位置で、ドライブのトルクまたは力は同じになります。

ジョイント	結果のトルク/力
アーム1	アーム 1 は回転軸であるため、結果はトルクになります。 `M1=0 Nm`.
アーム 2	アーム 2 は回転軸であるため、結果はトルクになります。 `M2=0 Nm`.
Z軸	Z 軸はプリズム軸であるため、結果は力になります。 `F3=m3*g N`重力加速度で `g`.

このセクションの内容:

動的ロボットモデル

アプリケーションの構造

パート 1: アプリケーションでの動的モデルの使用

パート 2: 動的ロボット モデルの作成

検索結果

パート 2: 動的ロボットモデルの作成