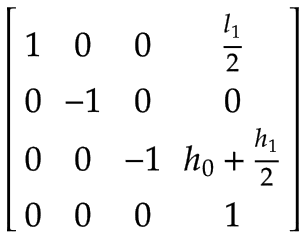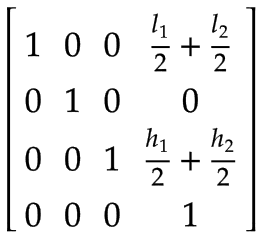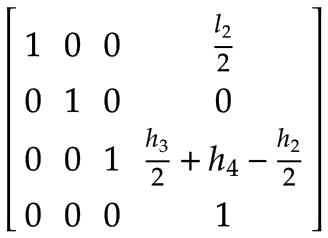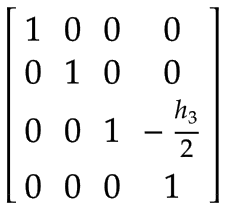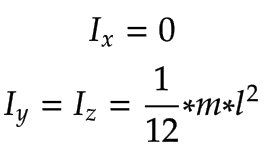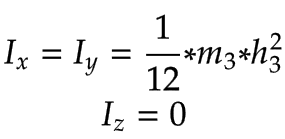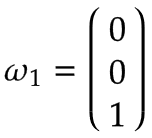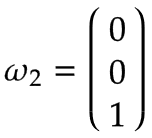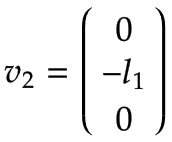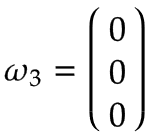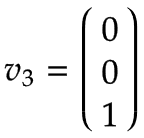Skip to main content

动态机器人模型

见 Robotics_DynamicModel.project 安装目录下的示例工程 CODESYS 在下面 ..\CODESYS SoftMotion\Examples.

为了限制运动期间的轴扭矩/力，需要一个动态模型，该模型根据当前轴状态（位置、速度和加速度）计算这些值。本示例包括以下部分：

  • 第 1 部分展示了如何在应用程序中使用现有的动态模型以及一些示例运动的结果。

  • 第 2 部分展示了如何根据 KM Lynch 和 FC Park 所著的《现代机器人》一书中提出的算法为 SCARA 机器人创建动态模型。

应用程序的结构

第 1 部分：在应用程序中使用动态模型

  • 此部分的代码位于 TorqueLimitationDemo文件夹。

  • PLC_PRG 是主程序，其中包含触发测试动作的状态机。

  • 可以使用以下方式监控运动 Trace。

第 2 部分：创建动态机器人模型

  • 动态模型的代码位于 DynModel 文件夹。

  • DynModel_Scara2_Z 是SCARA机器人的动力学模型。

  • DynModel_Tests 运行所有测试 Test_DynModel_Scara2_Z 检查常见错误。

  • 动力学模型基于具有两个旋转关节和一个棱柱 Z 轴的 SCARA 机器人。具有动态模型所需尺寸和坐标系的机器人图如下所示：

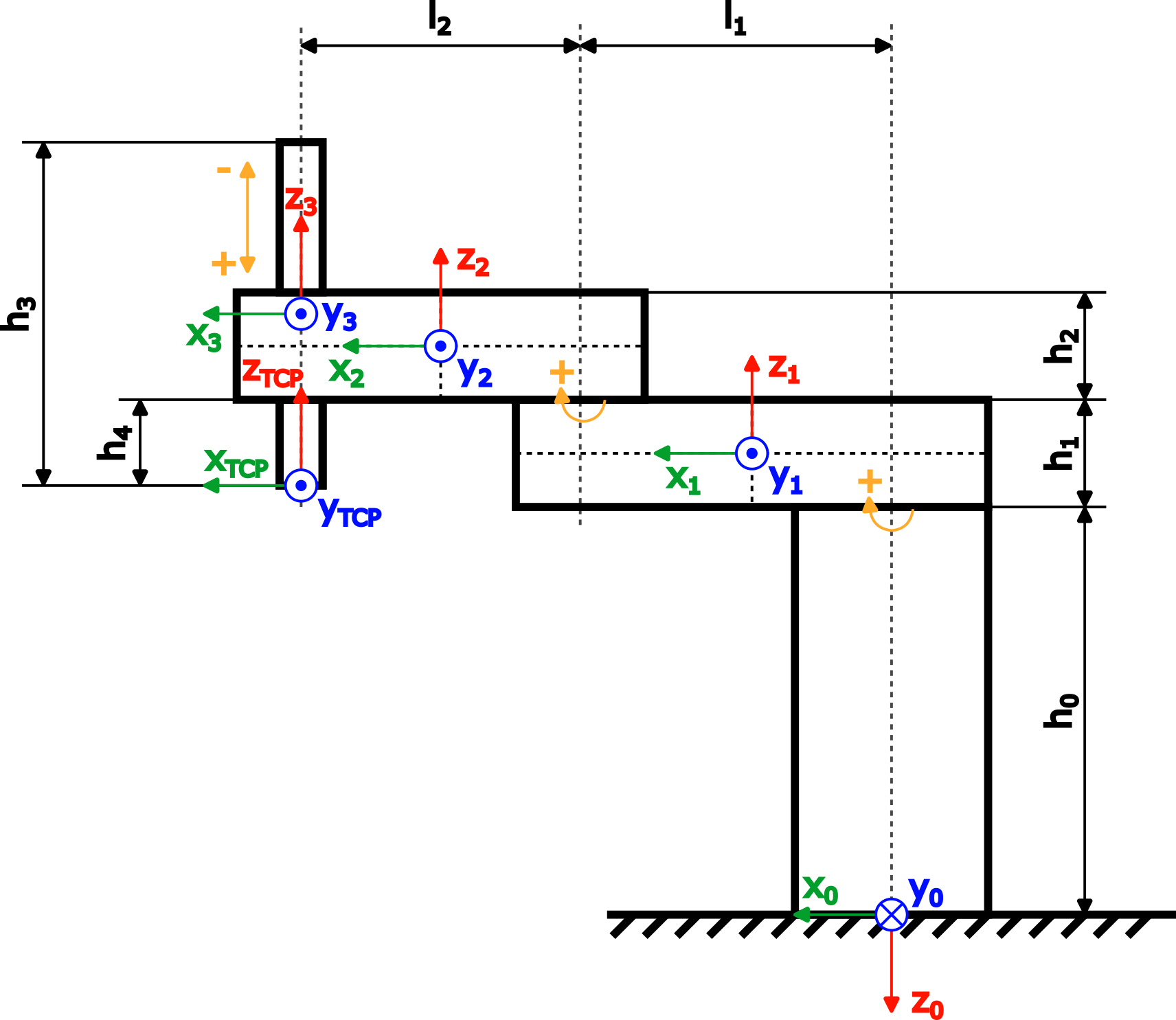
    _sm_img_dynmodel_scara_2_z.png

    图中尺寸

    功能块DynModel_Scara2_Z中样例工程中对应的变量名

    h0

    baseHeight

    h1

    armOneHeight

    h2

    armTwoHeight

    h3

    zAxisLength

    h4

    zAxisOffset

    l1

    armOneLength

    l1

    armTwoLength

第 1 部分：在应用程序中使用动态模型

在应用程序中使用动态模型需要一个模型来实现 ISMDynamics 的界面 SM3_Dynamics 图书馆。动态模型来自 第 2 部分：创建动态机器人模型 用于此演示。

可以使用将模型分配给轴组 SMC_GroupSetDynamics.此步骤需要设置相对于 MCS 的重力加速度。因为本例中的 SCARA 安装在地板上，所以重力加速度指向正 z0 方向。重力加速度必须以用户单位 u/s² 指定。由于此示例中的所有长度均以用户单位 m 定义，因此重力加速度也必须以 m/s² 为单位指定。

SMC_ChangeDynamicLimits 可用于调整每个轴的限制。请注意，必须使用再次启用轴组 MC_GroupEnable 为了激活新的动态限制。

如果向 TCP 添加额外的质量（例如，机器人拾取的工具或物体），则 SMC_GroupSetLoad 可用于定义负载。

这 PLC_PRG 程序包含上述所有组件并执行两个测试动作：

运动 1

运动 2

从 (a0=0°, a1=0°, a2=0 m) 到 (a0=90°, a1=0°, a2=0,02 m) 的直臂运动：

_sm_img_dynmodel_one.png

从 (a0=0°, a1=-120°, a2=0 m) 到 (a0=90°, a1=-120°, a2=0,02 m) 的角度臂运动：

_sm_img_dynmodel_two.png

每个运动连续执行三次，边界条件如下：

  • 所有轴的扭矩限制是无限的（unlimited）。

  • 第 2 臂的扭矩限制设置为低于无限移动期间达到的最大扭矩的值。该值被任意设置为 2 Nm.

  • Arm 2 的扭矩限制仍然是 2 Nm，另外在 TCP 处施加了负载（mLoad=3 kg, lLoad=0.2 m):

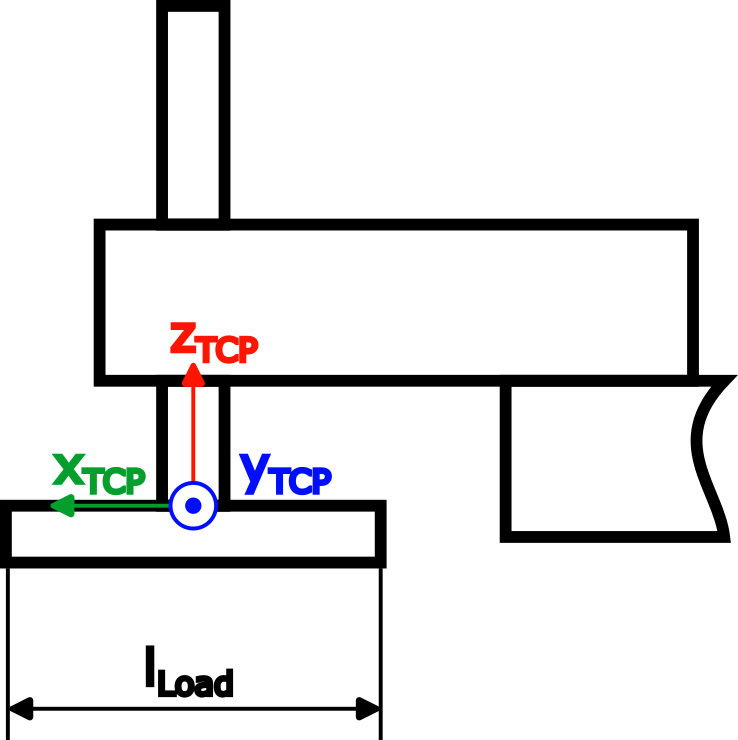_sm_img_robot_with_load.png

使用细杆简化了负载的惯量计算：

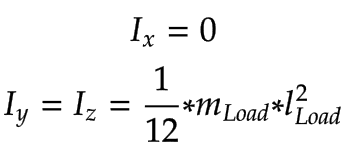_sm_img_load_inertia_tensor.png

可以在轨迹中监控运动。运动 1 具有以下结果：

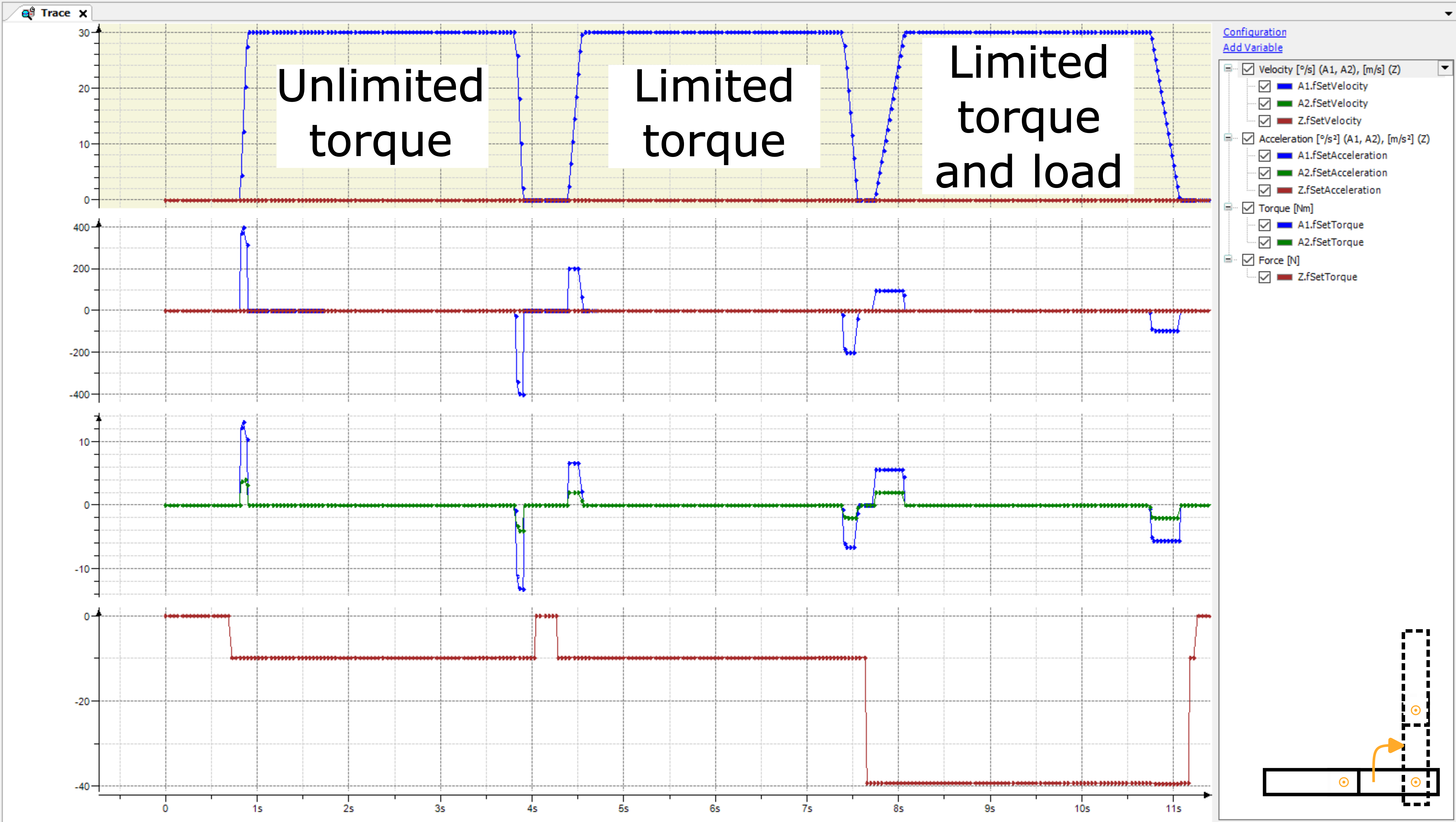
_sm_img_movement_one_results.png

  • 即使在运动 1 期间手臂 2 不移动，手臂 1 的运动也会在加速/减速期间为手臂 2 产生扭矩。计算出的扭矩被发送到驱动器，并可能改进控制器模式下的控制器回路 SMC_velocity 或者 SMC_position.这也称为转矩前馈控制。

  • 以有限扭矩进行的第二次运行表明，即使 Arm 2 不移动，Arm 2 的扭矩限制也会减慢 Arm 1 的运动。如果没有动态模型，则必须手动减少 Arm 1 的加速度和减速度运动，以防止对第 2 臂施加过大的机械应力。

  • 第三次带负载运行会进一步减慢第 1 臂的运动速度，以免违反第 2 臂的扭矩限制。

使用动态模型的优势是显而易见的。在没有动态模型的情况下防止机械应力过大：

  • 要么必须根据机器人的当前状态设置每个运动的动态限制。

  • 或者所有轴的动态限制都必须降低，这样所有潜在的运动都不会导致任何轴上的机械应力过大。

第一种方法是一项复杂的任务，可能很难计算出合理的限制，而第二种方法导致的运动在大多数情况下并不尽可能快。动态模型不再存在这些缺点，因为机器人总是尽可能快地移动，同时仍然遵守每个轴的机械限制。

运动 2 的结果说明了这些优点：

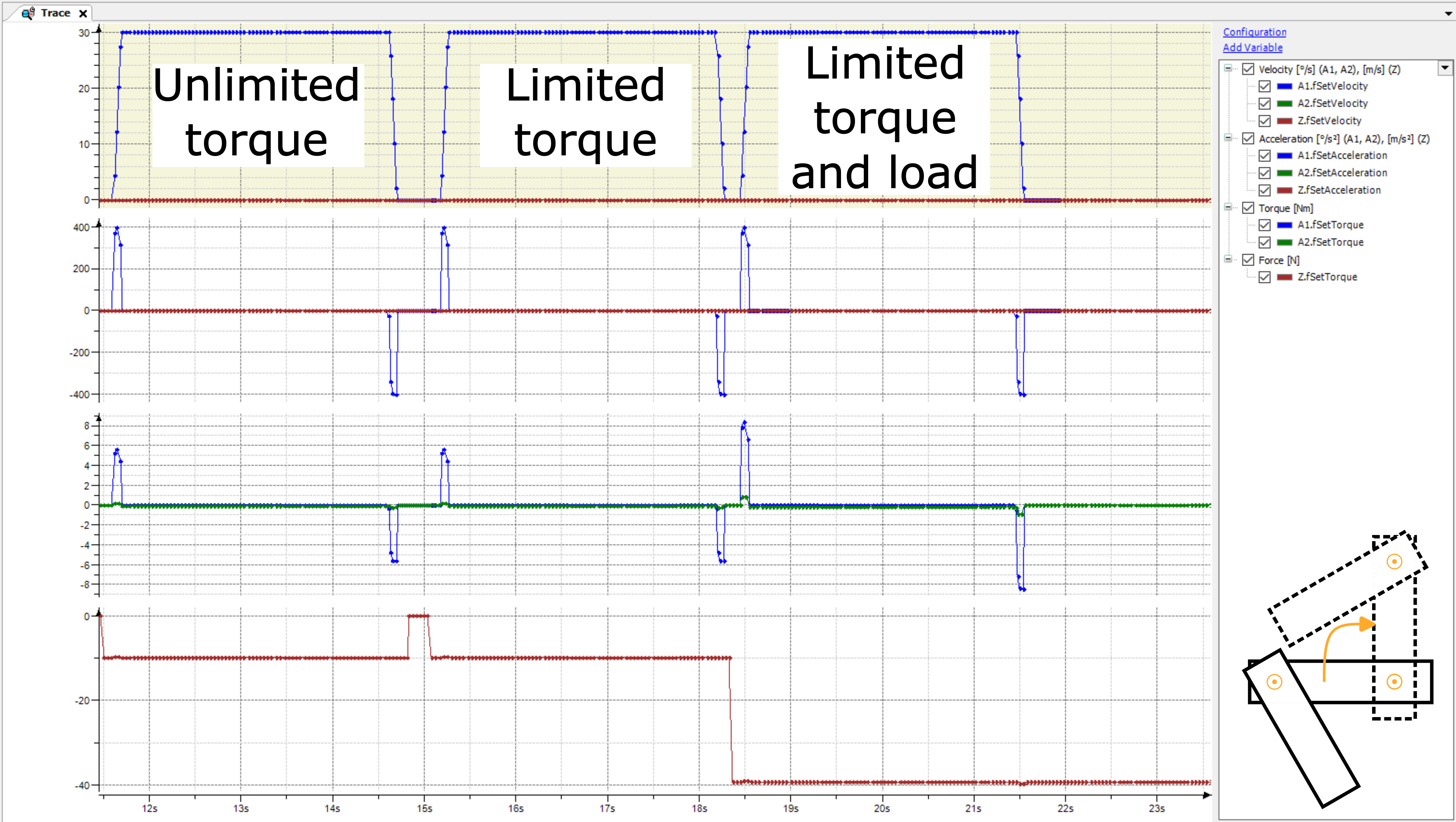
_sm_img_movement_two_results.png

由于倾斜的臂 2，臂 2 产生的扭矩远低于运动 1。因此，所有三个运行都不会受到轴扭矩的限制。如果使用基于运动 1 的调整动态限制（减少加速度和减速度以免违反手臂 2 的扭矩限制），则该运动会比必要的慢。

第 2 部分：创建动态机器人模型

本例中创建的模型基于 KM Lynch 和 FC Park 合着的“现代机器人”一书中介绍的开链机器人算法（参见第 8 章“开链动力学”）。这个算法的解释超出了这个例子的范围。相反，该示例侧重于如何定义算法的输入值。

简化

为了使这个例子更容易理解，做了一些简化：

  • 臂长 l1 和 l2 （旋转轴之间的距离）用作它们各自的总臂长。

  • 质心始终位于每个连杆的几何中心。

  • 计算细杆的臂和 Z 轴的空间惯性矩阵。

动态模型要求

为了在 SoftMotion 应用程序中使用动态模型，该模型必须实现 ISMDynamics 接口 SM3_Dynamics 图书馆。

动态模型的零位、坐标系、正旋转方向理论上都可以偏离运动学模型。但是，必须考虑这些差异，并且为了简化动态模型，因此建议使用运动学模型的定义。

由于动态模型必须计算以 Nm 为单位的扭矩值和以 N 为单位的力，因此它必须将长度的用户单位 u 转换为 SI 单位 m。转换因子可以设置为 SMC_GroupSetUnits 并包含在 addParams 输入 ISMDynamics.AxesStateToTorque.此示例仅使用 m 作为长度，因此可以忽略转换因子。

模型的几何和动态数据的规范

KM Lynch 和 FC Park 在“现代机器人”一书中介绍的算法的 IEC 实现（参见第 8 章“开放链动力学”）需要以下输入值：

  • 当机器人处于起始位置时每个连杆的质心位置。该位置在前一个链接的坐标系中指定（第一个链接是相对于基础坐标系指定的）。

  • 每个连杆的空间惯性矩阵和质量，以各自的连杆框架表示。

  • 各关节的螺丝轴，以基架表示。

质心位置

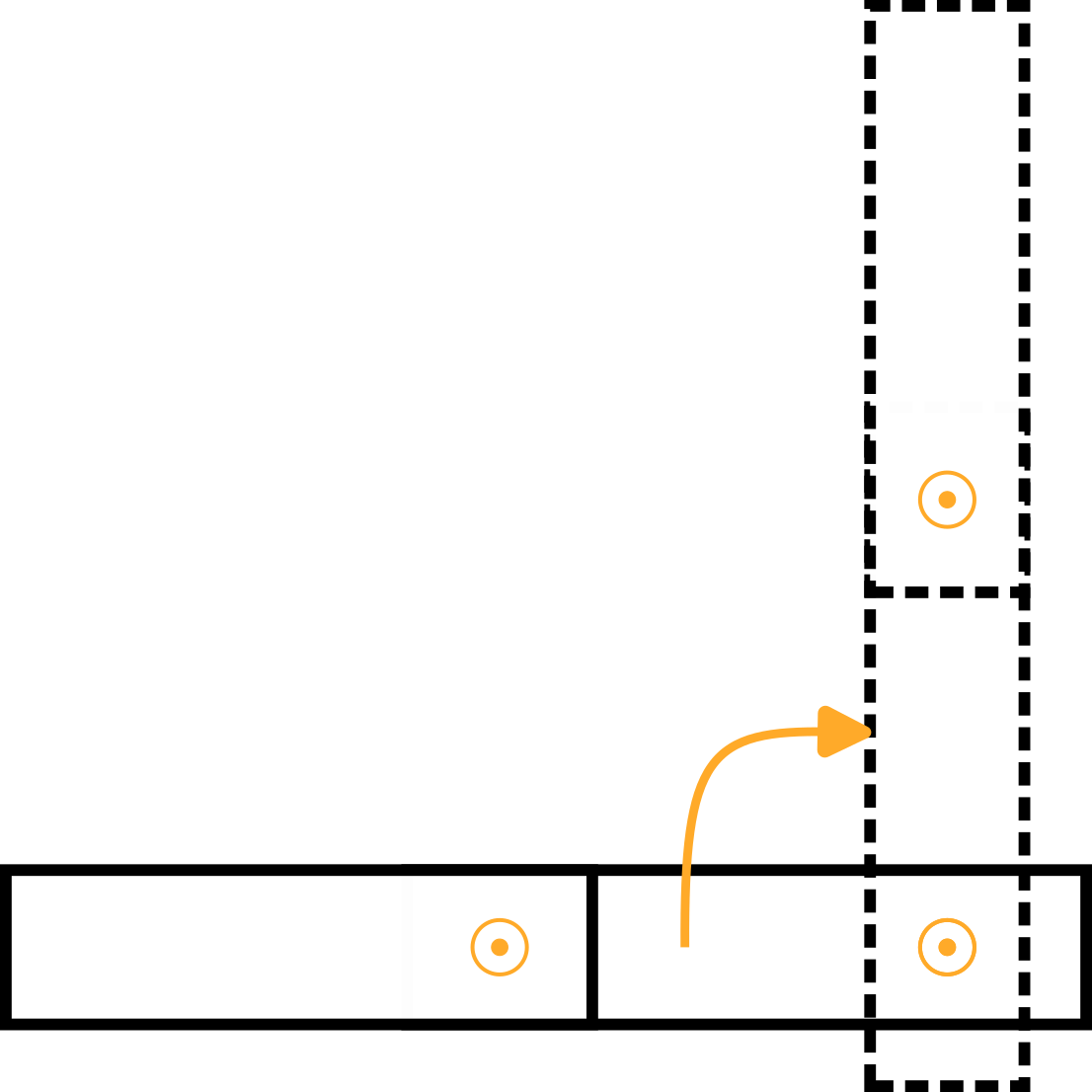
各连杆质心位置的框架如下：

关联

框架

手臂 1

手臂 1 的质心，以基本坐标系 x 表示0, 是0, z0:

_sm_img_arm1_centerofmass_frame.png

请注意，绕 x0 轴旋转了 180°。

手臂 2

Arm 2 的质心，在 Arm 1 的坐标系中表示：

_sm_img_arm2_centerofmass_frame.png

Z轴

在 Arm 2 的坐标系中表示的 Z 轴质心：

_sm_img_zaxis_centerofmass_frame.png

工具中心点 (TCP)

一个额外的框架来处理 TCP 处的任意负载（例如，通过工具、产品或两者的组合），以 Z 轴的坐标系表示：

_sm_img_externalforce_centerofmass_frame.png

空间惯性矩阵

空间惯性值必须在相应的链接框架中表示。由于框架定义在质心，空间惯性可以用 3x3 旋转惯性矩阵和物体的质量来表示。

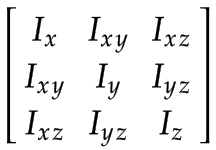_sm_img_general_inertia_tensor.png

通过使用细杆作为关节进行简化，转动惯量矩阵的分量如下：

关联

空间惯性矩阵

第 1 臂，第 2 臂

手臂 1 和手臂 2 及其相应的质量 m1 和 m2, 和长度 l1 和 l2:

_sm_img_arm1_arm2_inertiatensor.png

Z轴

_sm_img_zaxis_inertiatensor.png

螺旋轴

所有关节的螺旋轴必须相对于基本坐标系 x 表示0, 是0, z0.

关联

螺杆轴

手臂 1

想象一个转盘以 1 rad/s 的角速度沿正方向围绕关节 1 旋转。

在基础坐标系中表示，这是围绕z的正向旋转0-轴根据右手法则：

_sm_img_arm1_screwaxis_angularvelocity.png

因为Arm 1的旋转轴等于基础坐标系的中心，所以线速度为零：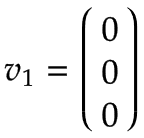

_sm_arm1_screwaxis_linearvelocity.png

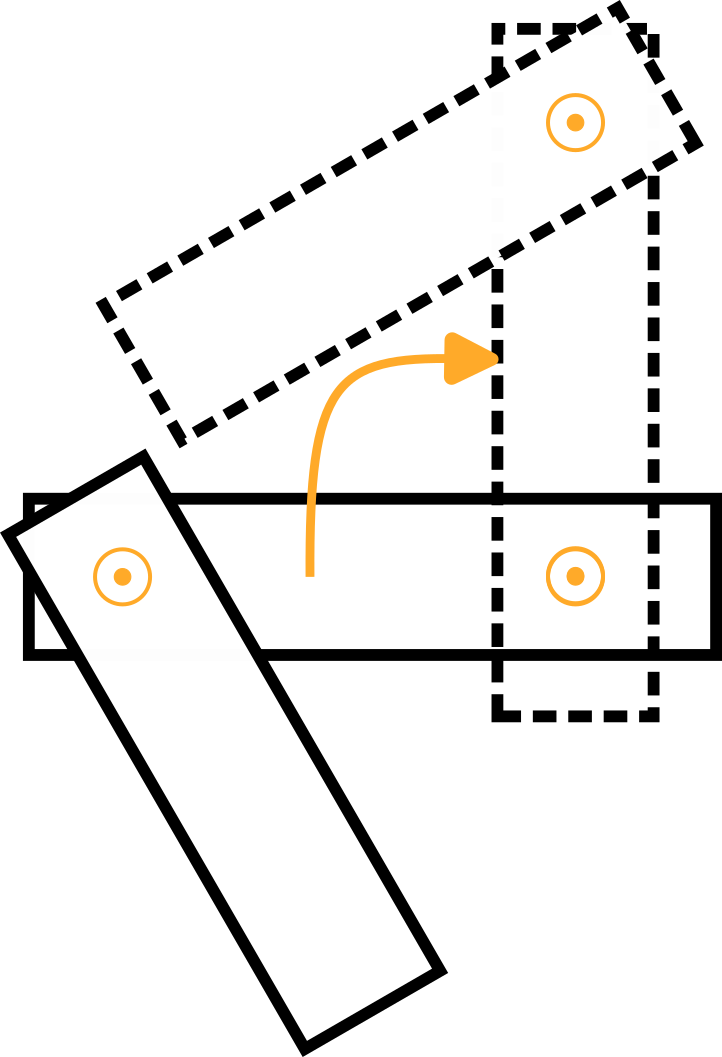
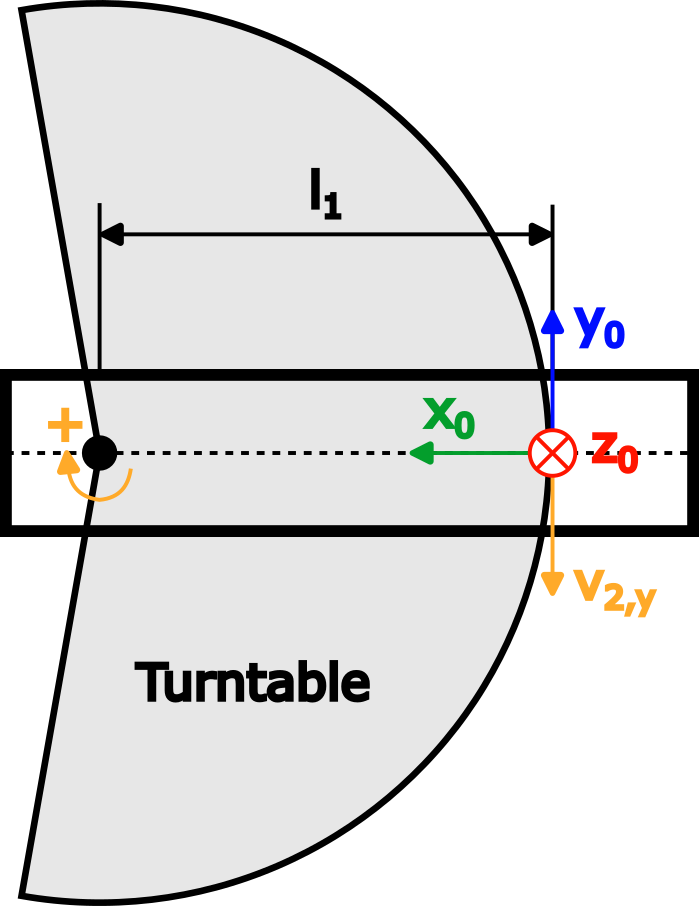
手臂 2

同样，想象一个转盘以 1 rad/s 的角速度正向围绕关节 2 旋转，如下图所示，它显示在机械臂 1 的顶视图中：

_sm_img_arm2_screwaxis.png

对于 Arm 1，角速度为：

_sm_img_arm2_screwaxis_angularvelocity.png

该图显示了由此产生的线速度 v2,y, 指向负 y0 方向并且等于 v2,y=-ω2,z * l1个.

_sm_img_arm2_screwaxis_linearvelocity.png

Z轴

Z 轴是棱柱轴，适用以下规则：

  • 角速度矢量 ω 为零。

  • 线速度矢量是正平移方向上的单位矢量。

这导致以下向量，以基本坐标系 x 表示0, 是0, z0:

_sm_img_zaxis_screwaxis_angularvelocity.png
_sm_img_zaxis_screwaxis_linearvelocity.png

测试

现在可以测试动态模型，因为所有模型参数都已定义。本节包括模型的一些基本测试。

检查丝杠轴

螺杆轴 S 具有角速度 ω 和线速度 v 可以表示为一个元素 se(3):

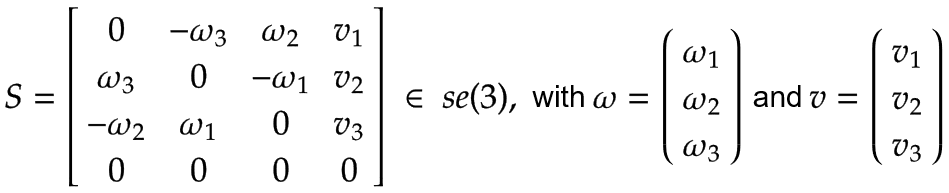_sm_img_screwaxis_se3.png

正向转型 T 可以用螺旋轴执行 S, 末端执行器框架 M 对于机器人的零位置，以及关节角度 θ 每个关节：

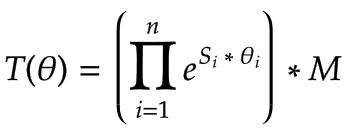_sm_img_screwaxis_forwardtransformation.png

示例项目已经包含一个求解该方程的函数（请参阅 SMC_OpenChainKinematics_SolveForward).有关详细信息，请参阅 KM Lynch 和 FC Park 合着的《现代机器人》一书。

使用正向变换方程，现在可以使用已知轴位置运行测试并检查变换是否导致预期结果。

检查静止时的扭矩计算

要检查质心位置框架，您可以手动计算给定轴位置的静止轴扭矩，并将其与模型计算的值进行比较。由于此示例基于安装在地板上的 SCARA 机器人，因此所有静止轴位置都将导致相同的驱动器扭矩或力：

联合的

产生的扭矩/力

手臂 1

因为 Arm 1 是旋转轴，所以结果是扭矩： M1=0 Nm.

手臂 2

因为 Arm 2 是旋转轴，所以结果是扭矩： M2=0 Nm.

Z轴

因为 Z 轴是棱柱轴，所以结果是一个力： F3=m3*g N重力加速度 g.

本节内容如下: