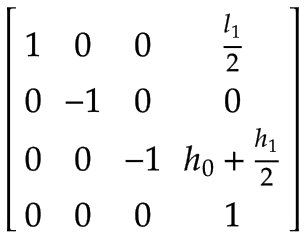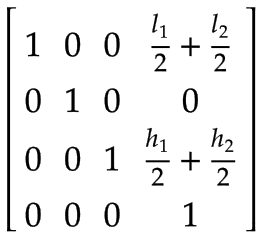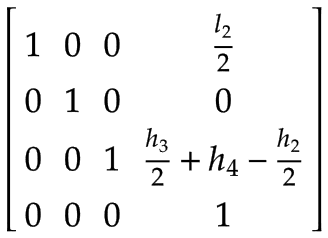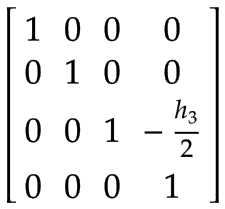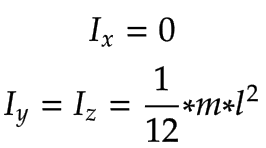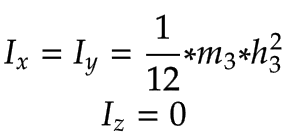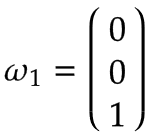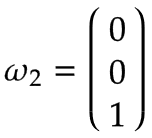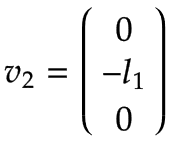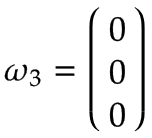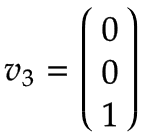Modello di robot dinamico
Vedi il Robotics_DynamicModel.project progetto di esempio nella directory di installazione di CODESYS sotto ..\CODESYS SoftMotion\Examples.
Per limitare le coppie/forze dell'asse durante un movimento, è necessario un modello dinamico che calcoli questi valori dallo stato attuale dell'asse (posizione, velocità e accelerazione). Questo esempio include le seguenti parti:
La parte 1 mostra come utilizzare un modello dinamico esistente in un'applicazione e i risultati di alcuni movimenti di esempio.
La parte 2 mostra come creare un modello dinamico per un robot SCARA basato su un algoritmo presentato nel libro "Modern Robotics" di KM Lynch e FC Park.
Struttura dell'applicazione
Parte 1: utilizzo di un modello dinamico in un'applicazione
Il codice per questa parte si trova nel file
TorqueLimitationDemocartella.PLC_PRGè il programma principale, che include una macchina a stati che attiva i movimenti di prova.I movimenti possono essere monitorati utilizzando il
Trace.
Parte 2: creazione di un modello di robot dinamico
Il codice per il modello dinamico si trova nel file
DynModelcartella.DynModel_Scara2_Zè il modello dinamico del robot SCARA.DynModel_Testsesegue tutti i test diTest_DynModel_Scara2_Zper verificare gli errori comuni.Il modello dinamico si basa su un robot SCARA con due giunti rotanti e un asse Z prismatico. Di seguito è mostrata una figura del robot con le dimensioni e i sistemi di coordinate richiesti per il modello dinamico:

Dimensione in figura
Nome variabile corrispondente nel progetto di esempio nel blocco funzione DynModel_Scara2_Z
h0baseHeighth1armOneHeighth2armTwoHeighth3zAxisLengthh4zAxisOffsetl1armOneLengthl1armTwoLength
Parte 1: utilizzo di un modello dinamico in un'applicazione
L'utilizzo di un modello dinamico in un'applicazione richiede un modello che implementi il ISMDynamics interfaccia del SM3_Dynamics biblioteca. Il modello dinamico da Parte 2: creazione di un modello di robot dinamico viene utilizzato per questa dimostrazione.
Il modello può essere assegnato a un gruppo di assi utilizzando SMC_GroupSetDynamics. Questo passaggio richiede l'impostazione dell'accelerazione gravitazionale rispetto al MCS. Poiché lo SCARA in questo esempio è montato sul pavimento, l'accelerazione gravitazionale punta nella direzione positiva z0. L'accelerazione gravitazionale deve essere specificata in unità utente u/s². Poiché tutte le lunghezze in questo esempio sono state definite nell'unità utente m, anche l'accelerazione gravitazionale deve essere specificata in m/s².
SMC_ChangeDynamicLimits può essere utilizzato per regolare i limiti di ciascun asse. Si noti che il gruppo di assi deve essere nuovamente abilitato utilizzando MC_GroupEnable per attivare i nuovi limiti dinamici.
Se vengono aggiunte ulteriori masse al TCP (ad esempio, uno strumento o un oggetto che viene raccolto dal robot), allora SMC_GroupSetLoad può essere utilizzato per definire il carico.
Il PLC_PRG programma contiene tutti i componenti di cui sopra ed esegue due movimenti di prova:
Movimento 1 | Movimento 2 | ||
|---|---|---|---|
Movimento del braccio rettilineo da (a0=0°, a1=0°, a2=0 m) a (a0=90°, a1=0°, a2=0,02 m):
| Movimento del braccio inclinato da (a0=0°, a1=-120°, a2=0 m) a (a0=90°, a1=-120°, a2=0,02 m):
|
Ogni movimento viene eseguito tre volte consecutive con le seguenti condizioni al contorno:
Il limite di coppia di tutti gli assi è infinito (illimitato).
Il limite di coppia del braccio 2 è impostato su un valore inferiore alla coppia massima raggiunta durante il movimento illimitato. Il valore è stato arbitrariamente impostato su
2 Nm.Il limite di coppia del braccio 2 è fermo
2 Nm, e inoltre è stato applicato un carico al TCP (mLoad=3 kg,lLoad=0.2 m):
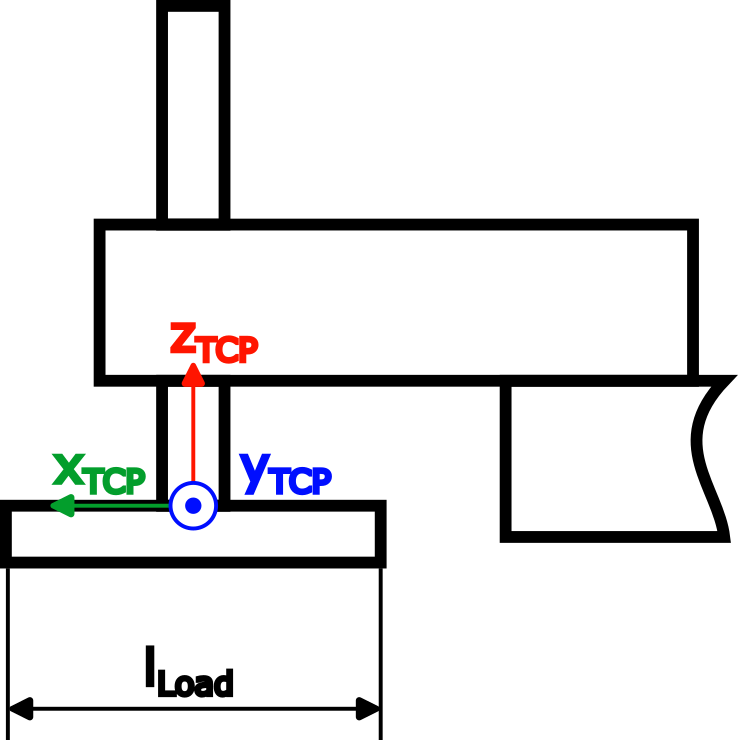 |
Il calcolo dell'inerzia per il carico è stato semplificato utilizzando barre sottili:
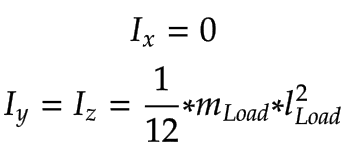 |
I movimenti possono essere monitorati nella traccia. Il movimento 1 ha i seguenti risultati:
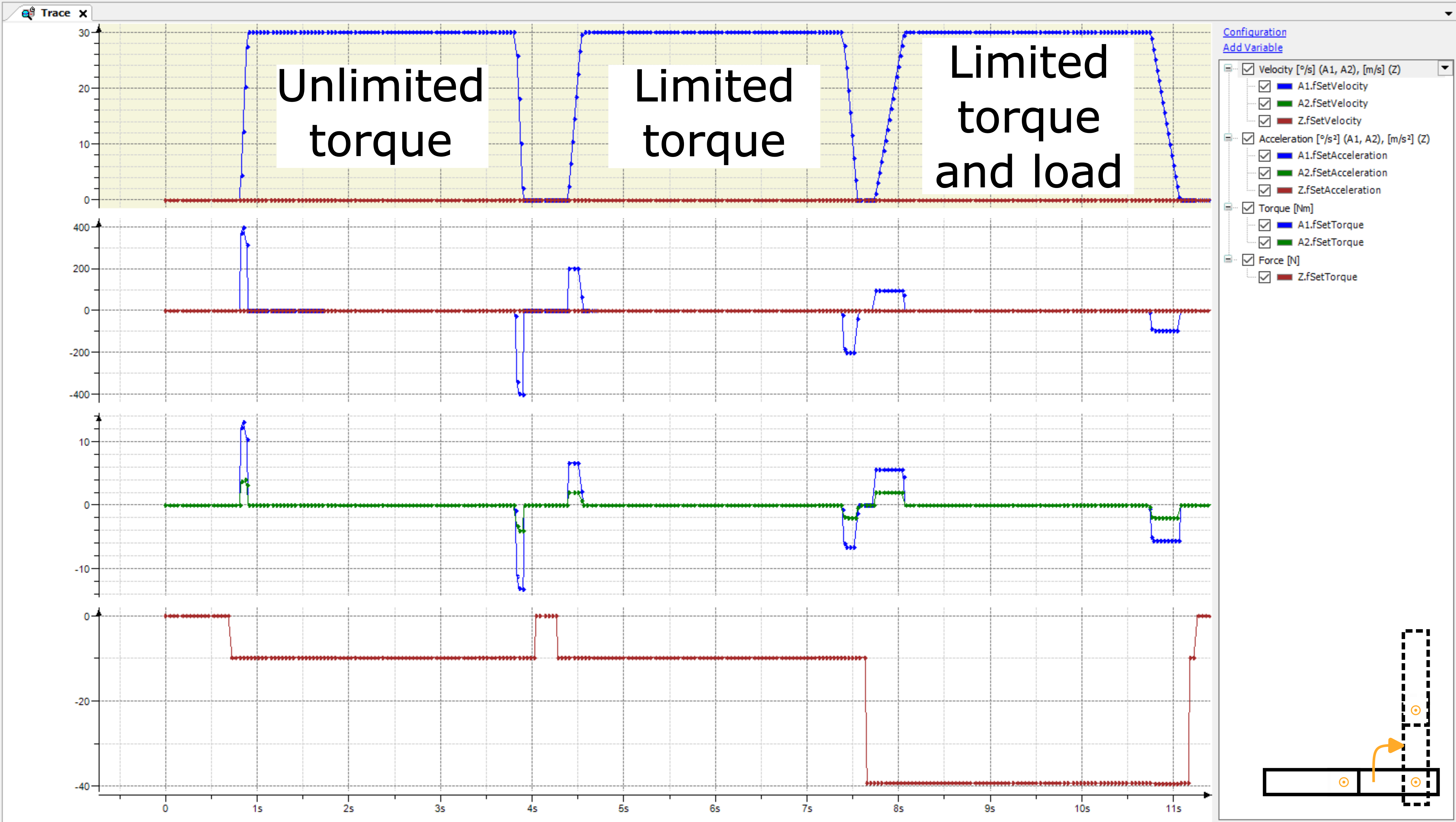
Anche se il braccio 2 non si muove durante il movimento 1, il movimento del braccio 1 provoca una coppia per il braccio 2 durante l'accelerazione/decelerazione. La coppia calcolata viene inviata all'azionamento e può potenzialmente migliorare il loop del controller in modalità controller
SMC_velocityoSMC_position. Questo è anche chiamato controllo feed forward della coppia.La seconda corsa con coppia limitata mostra che anche se il braccio 2 non si muove, un limite di coppia per il braccio 2 rallenta il movimento del braccio 1. Senza il modello dinamico, l'accelerazione e la decelerazione del braccio 1 dovrebbero essere ridotte manualmente per questo movimento per evitare eccessive sollecitazioni meccaniche sul braccio 2.
La terza corsa con un carico rallenta ancora di più il movimento del braccio 1 per non violare il limite di coppia del braccio 2.
I vantaggi dell'utilizzo di un modello dinamico sono evidenti. Per evitare sollecitazioni meccaniche eccessive senza modello dinamico:
O i limiti dinamici per ogni movimento dovrebbero essere impostati a seconda dello stato attuale del robot.
Oppure i limiti dinamici di tutti gli assi dovrebbero essere ridotti in modo tale che tutti i potenziali movimenti non portino a sollecitazioni meccaniche eccessive su alcun asse.
Il primo metodo è un compito complesso e può essere difficile calcolare limiti ragionevoli, mentre il secondo metodo si traduce in movimenti che non sono il più veloci possibile per la maggior parte del tempo. Questi inconvenienti non esistono più con un modello dinamico perché il robot si muove sempre il più velocemente possibile pur rispettando i limiti meccanici di ciascun asse.
Questi vantaggi sono illustrati dai risultati del Movimento 2:
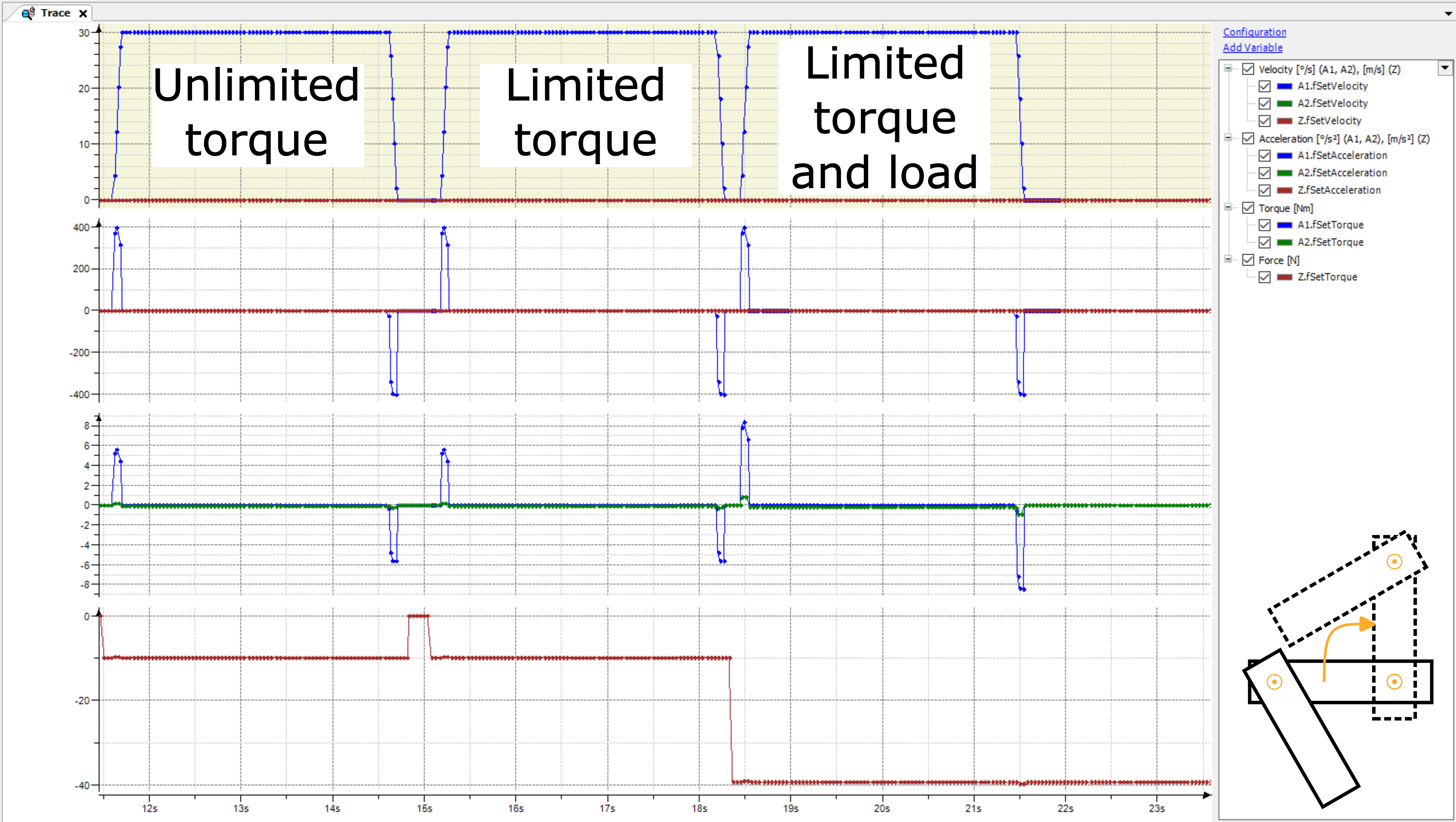
A causa del Braccio 2 angolato, la coppia risultante del Braccio 2 è notevolmente inferiore a quella del Movimento 1. Pertanto, tutte e tre le corse non sono mai limitate dalla coppia dell'asse. Se si fossero utilizzati limiti dinamici adattati basati sul Movimento 1 (accelerazione e decelerazione ridotte per non violare il limite di coppia del Braccio 2), allora questo movimento sarebbe stato più lento del necessario.
Parte 2: creazione di un modello di robot dinamico
Il modello creato in questo esempio si basa su un algoritmo per robot a catena aperta presentato nel libro "Modern Robotics" di KM Lynch e FC Park (vedere il capitolo 8 "Dynamics of Open Chains"). La spiegazione di questo algoritmo va oltre lo scopo di questo esempio. Invece, l'esempio si concentra su come definire i valori di input dell'algoritmo.
Semplificazioni
Per rendere più comprensibile questo esempio, sono state apportate alcune semplificazioni:
Le lunghezze delle braccia
l1el2(distanza tra gli assi di rotazione) vengono utilizzati come rispettiva lunghezza totale del braccio.Il centro di massa si trova sempre nel centro geometrico di ciascun collegamento.
Le matrici di inerzia spaziale dei bracci e dell'asse Z sono calcolate per aste sottili.
Requisiti del modello dinamico
Per utilizzare il modello dinamico in un'applicazione SoftMotion, questo modello deve implementare il file ISMDynamics interfaccia del SM3_Dynamics biblioteca.
La posizione zero, i sistemi di coordinate e il senso di rotazione positivo del modello dinamico possono discostarsi teoricamente dal modello cinematico. Tuttavia, queste differenze devono essere prese in considerazione e, per semplificare il modello dinamico, si raccomanda quindi di utilizzare le definizioni del modello cinematico.
Poiché il modello dinamico deve calcolare i valori della coppia in Nm e le forze in N, deve convertire l'unità utente u per le lunghezze in unità SI m. Il fattore di conversione può essere impostato da SMC_GroupSetUnits ed è incluso nel addParams ingresso di ISMDynamics.AxesStateToTorque. Questo esempio usa solo m per le lunghezze e può quindi ignorare il fattore di conversione.
Specifica dei dati geometrici e dinamici del modello
L'implementazione IEC dell'algoritmo presentato nel libro "Modern Robotics" di KM Lynch e FC Park (vedi capitolo 8 "Dynamics of Open Chains") richiede i seguenti valori di input:
La posizione del centro di massa di ciascun collegamento quando il robot è nella posizione iniziale. La posizione è specificata nel sistema di coordinate del collegamento precedente (il primo collegamento è specificato rispetto al sistema di coordinate di base).
La matrice di inerzia spaziale e la massa di ciascun collegamento, espresse nel rispettivo frame di collegamento.
L'asse della vite di ciascun giunto, espresso nel telaio di base.
Posizioni del centro di massa
I fotogrammi con la posizione del baricentro di ciascun collegamento sono i seguenti:
Collegamento | Telaio | |
|---|---|---|
Braccio 1 | Il centro di massa del braccio 1, espresso nel sistema di coordinate di base x0, e0, z0:
Si noti che c'è una rotazione di 180° attorno all'asse x0. | |
Braccio 2 | Il centro di massa del braccio 2, espresso nel sistema di coordinate del braccio 1:
| |
Asse Z | Il centro di massa dell'asse Z espresso nel sistema di coordinate del braccio 2:
| |
Punto centrale dell'utensile (TCP) | Un frame aggiuntivo per gestire un carico arbitrario sul TCP (ad esempio, da uno strumento, un prodotto o una combinazione di entrambi), espresso nel sistema di coordinate dell'asse Z:
|
Matrici di inerzia spaziale
I valori di inerzia spaziale devono essere espressi nel rispettivo frame di collegamento. Poiché i telai sono definiti al centro di massa, l'inerzia spaziale può essere rappresentata da una matrice di inerzia rotazionale 3x3 e dalla massa del corpo.
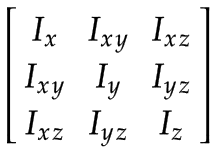 |
Con la semplificazione dell'utilizzo di aste sottili per i giunti, i componenti della matrice di inerzia rotazionale sono i seguenti:
Collegamento | Matrice di inerzia spaziale | |
|---|---|---|
Braccio 1, Braccio 2 | Braccio 1 e Braccio 2 con la massa corrispondente
| |
Asse Z |
|
Assi a vite
Gli assi delle viti di tutti i giunti devono essere espressi rispetto al sistema di coordinate di base x0, e0, z0.
Collegamento | Asse della vite | |||
|---|---|---|---|---|
Braccio 1 | Immagina una piattaforma girevole che ruota attorno al giunto 1 in direzione positiva con una velocità angolare di 1 rad/s. Espressa nel sistema di coordinate di base, questa è una rotazione positiva attorno alla z0-asse secondo la regola della mano destra:
Poiché l'asse di rotazione del braccio 1 è uguale al centro del sistema di coordinate di base, la velocità lineare è zero: 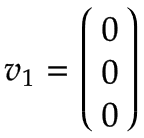 | |||
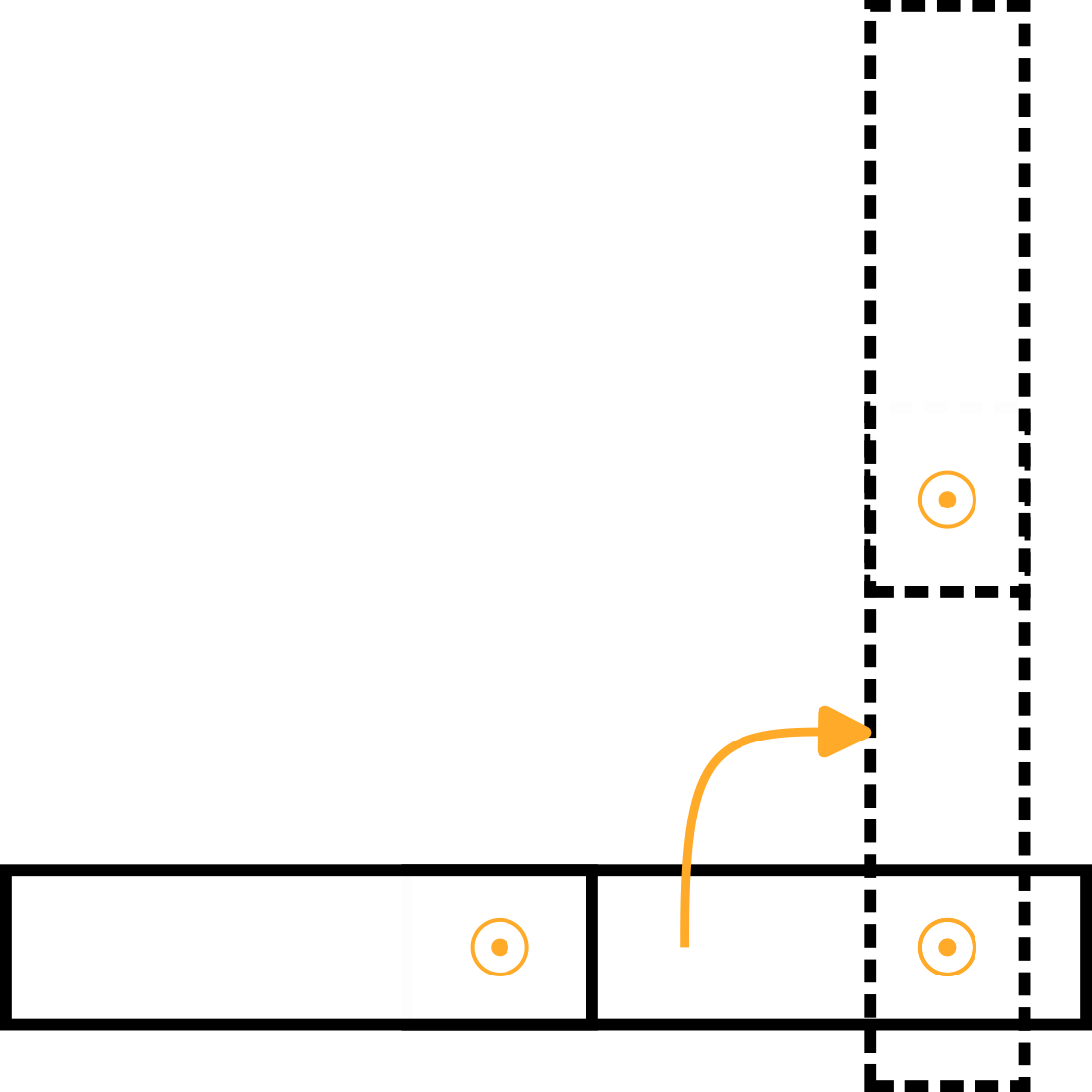
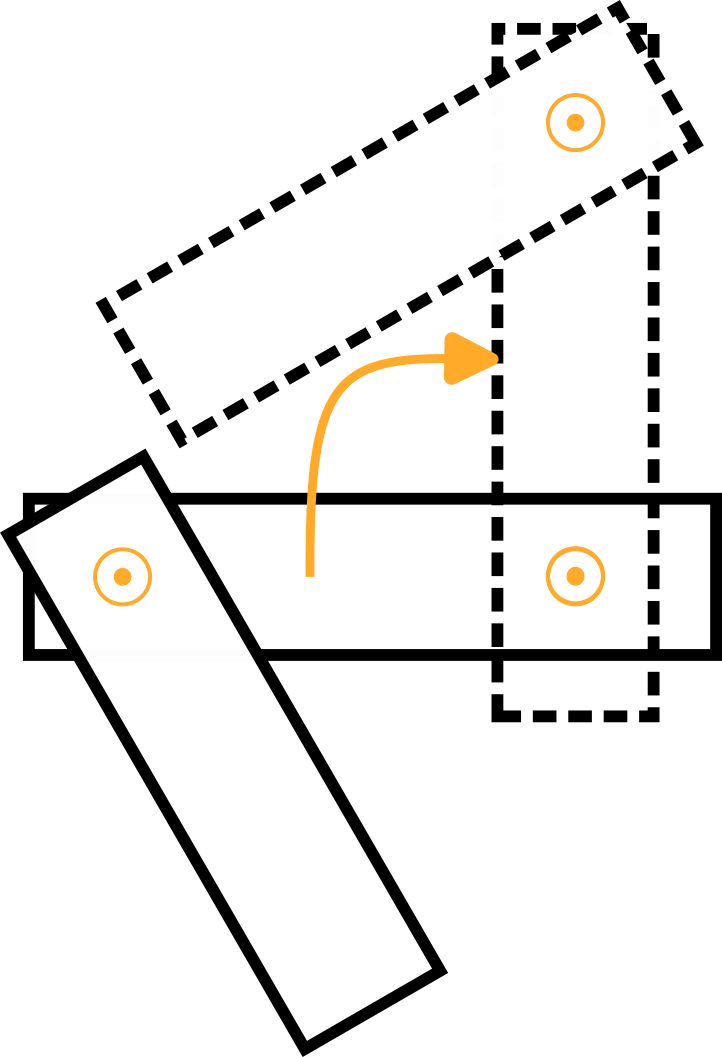
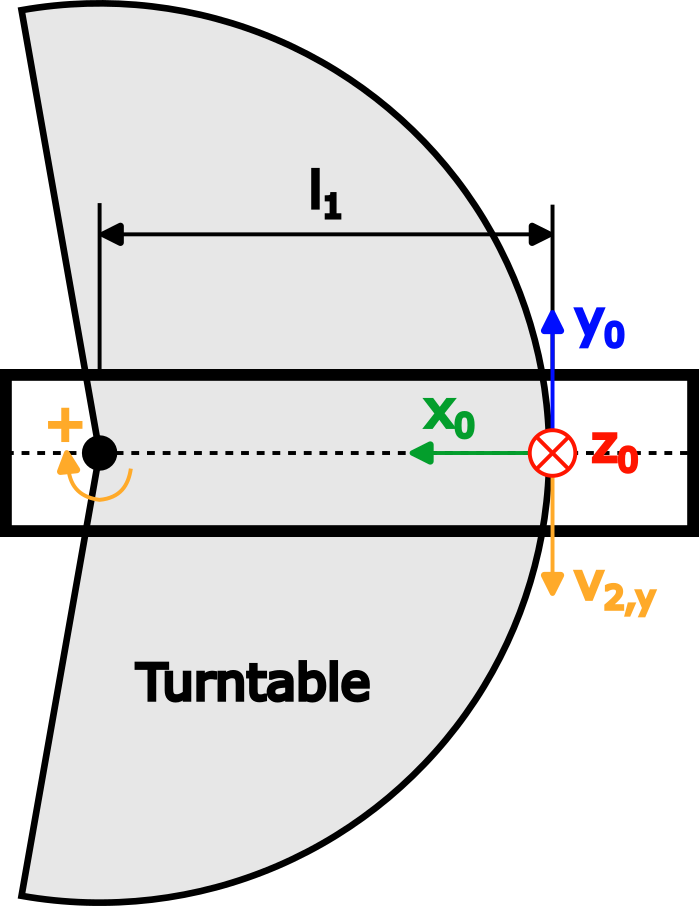
Braccio 2 | Ancora una volta, immagina una piattaforma girevole che ruota attorno al giunto 2 in direzione positiva con una velocità angolare di 1 rad/s, che viene visualizzata nella vista dall'alto del braccio 1 nella figura seguente:
Per quanto riguarda il braccio 1, la velocità angolare è:
La figura mostra la velocità lineare risultante v2,a, che indica y negativo0 direzione ed è uguale a v2,a=-ω2,z *l1.
| |||
Asse Z | L'asse Z è un asse prismatico per il quale si applicano le seguenti regole:
Questo porta ai seguenti vettori, espressi nel sistema di coordinate di base x0, e0, z0:
|
Test
Il modello dinamico può ora essere testato perché tutti i parametri del modello sono definiti. Questa sezione include alcuni test di base del modello.
Controllo degli assi della vite
Un asse a vite S con velocità angolare ω e velocità lineare v può essere espresso come un elemento di se(3):
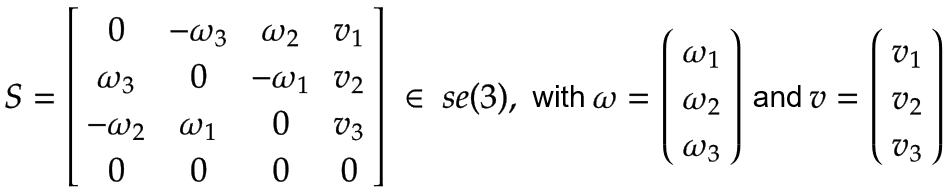 |
Una trasformazione in avanti T può essere eseguito con gli assi a vite S, un frame dell'effettore finale M per la posizione zero del robot e l'angolo del giunto θ di ogni giunto:
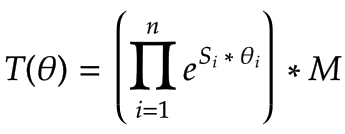 |
Il progetto di esempio include già una funzione che risolve questa equazione (vedi SMC_OpenChainKinematics_SolveForward). Per maggiori dettagli, vedere il libro "Modern Robotics" di KM Lynch e FC Park.
Utilizzando l'equazione di trasformazione in avanti, è ora possibile eseguire un test con posizioni degli assi note e verificare se la trasformazione porta al risultato atteso.
Controllo del calcolo della coppia da fermo
Per controllare il centro dei frame di posizione della massa, è possibile calcolare manualmente la coppia risultante dell'asse in stato di fermo per determinate posizioni dell'asse e confrontarle con i valori calcolati dal modello. Poiché questo esempio si basa su un robot SCARA montato a pavimento, tutte le posizioni degli assi in stato di fermo porteranno alle stesse coppie o forze degli azionamenti:
Giunto | Coppia/Forza risultante |
|---|---|
Braccio 1 | Poiché il braccio 1 è un asse di rivoluzione, il risultato è una coppia: |
Braccio 2 | Poiché il braccio 2 è un asse di rivoluzione, il risultato è una coppia: |
Asse Z | Poiché l'asse Z è un asse prismatico, il risultato è una forza: |