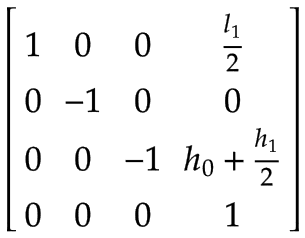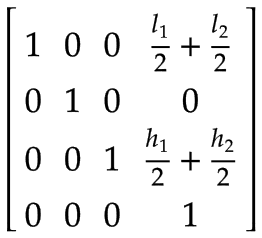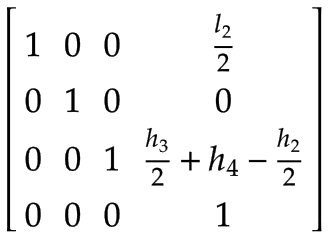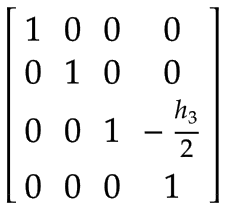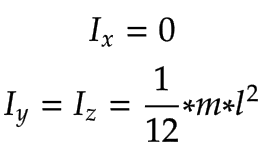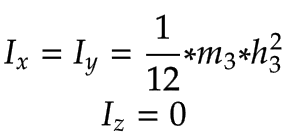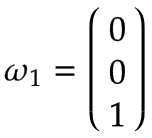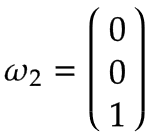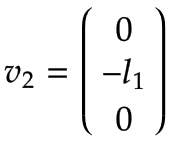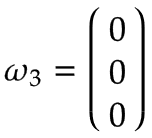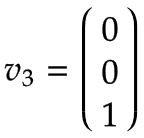Modèle de robot dynamique
Voir le Robotics_DynamicModel.project exemple de projet dans le répertoire d'installation de CODESYS en dessous de ..\CODESYS SoftMotion\Examples.
Afin de limiter les couples/forces de l'axe pendant un mouvement, un modèle dynamique est nécessaire qui calcule ces valeurs à partir de l'état actuel de l'axe (position, vitesse et accélération). Cet exemple comprend les pièces suivantes :
La première partie montre comment utiliser un modèle dynamique existant dans une application et les résultats de quelques exemples de mouvements.
La partie 2 montre comment créer un modèle dynamique pour un robot SCARA basé sur un algorithme présenté dans le livre "Modern Robotics" de KM Lynch et FC Park.
Structure de la demande
Partie 1 : Utiliser un modèle dynamique dans une application
Le code de cette pièce se trouve dans le
TorqueLimitationDemodossier.PLC_PRGest le programme principal, qui comprend une machine à états qui déclenche des mouvements de test.Les mouvements peuvent être surveillés à l'aide du
Trace.
Partie 2 : Création d'un modèle de robot dynamique
Le code du modèle dynamique se trouve dans le
DynModeldossier.DynModel_Scara2_Zest le modèle dynamique du robot SCARA.DynModel_Testsexécute tous les tests deTest_DynModel_Scara2_Zpour vérifier les erreurs courantes.Le modèle dynamique est basé sur un robot SCARA avec deux articulations tournantes et un axe Z prismatique. Une figure du robot avec les dimensions et les systèmes de coordonnées requis pour le modèle dynamique est illustrée ci-dessous :
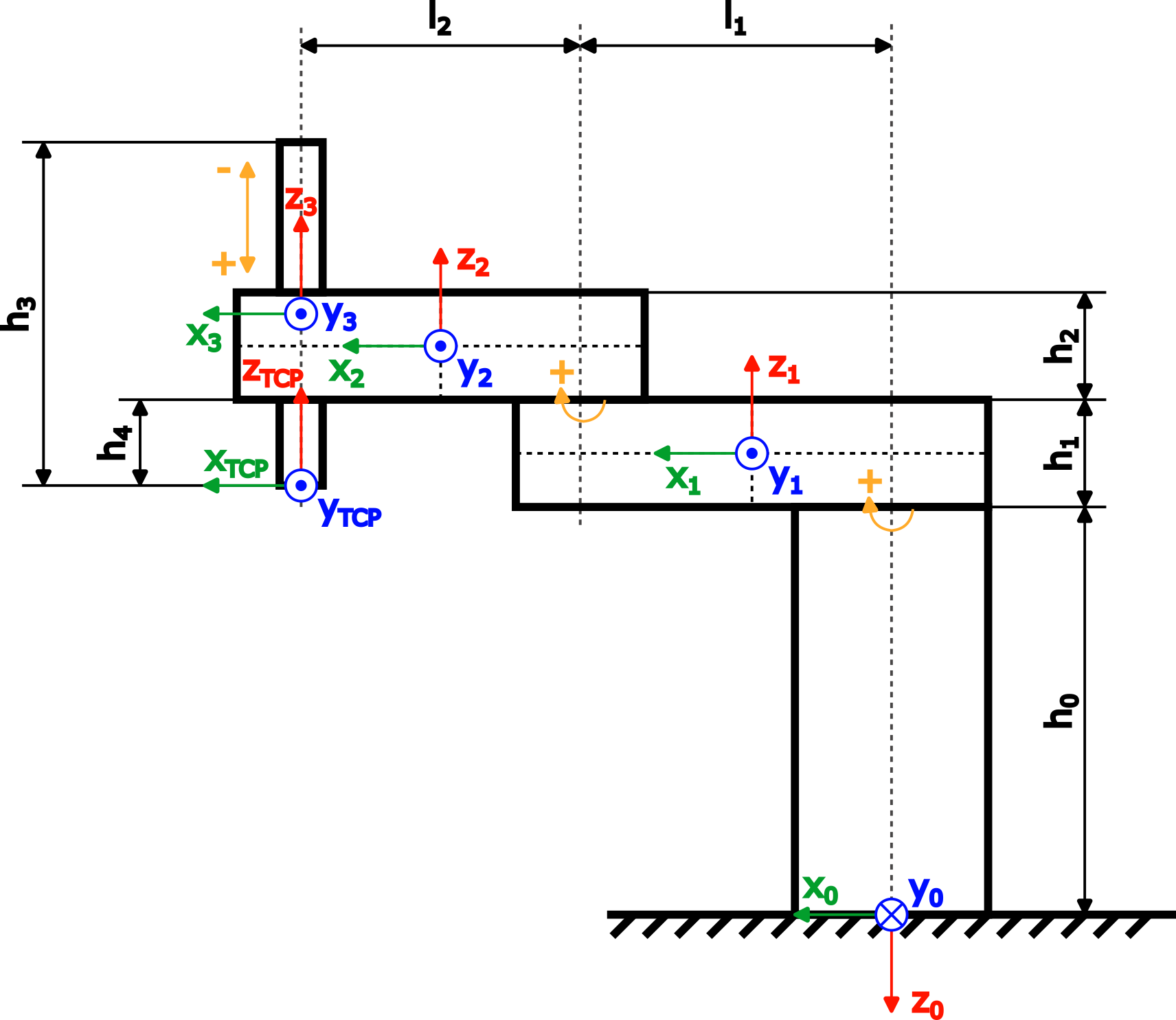
Dimension dans la figure
Nom de variable correspondant dans l'exemple de projet dans le bloc fonction DynModel_Scara2_Z
h0baseHeighth1armOneHeighth2armTwoHeighth3zAxisLengthh4zAxisOffsetl1armOneLengthl1armTwoLength
Partie 1 : Utiliser un modèle dynamique dans une application
L'utilisation d'un modèle dynamique dans une application nécessite un modèle qui implémente ISMDynamics interface de la SM3_Dynamics bibliothèque. Le modèle dynamique de Partie 2 : Création d'un modèle de robot dynamique est utilisé pour cette démonstration.
Le modèle peut être affecté à un groupe d'axes à l'aide de SMC_GroupSetDynamics. Cette étape nécessite la mise en place de l'accélération gravitationnelle par rapport au MCS. Parce que le SCARA dans cet exemple est monté sur le sol, l'accélération gravitationnelle pointe dans la direction z0 positive. L'accélération gravitationnelle doit être spécifiée en unités utilisateur u/s². Étant donné que toutes les longueurs dans cet exemple ont été définies dans l'unité utilisateur m, l'accélération gravitationnelle doit également être spécifiée en m/s².
SMC_ChangeDynamicLimits peut être utilisé pour ajuster les limites de chaque axe. Notez que le groupe d'axes doit être réactivé à l'aide de MC_GroupEnable afin d'activer les nouvelles limites dynamiques.
Si des masses supplémentaires sont ajoutées au TCP (par exemple, un outil ou un objet qui est ramassé par le robot), alors SMC_GroupSetLoad peut être utilisé pour définir la charge.
La PLC_PRG programme contient tous les composants ci-dessus et exécute deux mouvements de test :
Mouvement 1 | Mouvement 2 | ||
|---|---|---|---|
Mouvement droit du bras de (a0=0°, a1=0°, a2=0 m) à (a0=90°, a1=0°, a2=0,02 m) :
| Mouvement angulaire du bras de (a0=0°, a1=-120°, a2=0 m) à (a0=90°, a1=-120°, a2=0,02 m) :
|
Chaque mouvement est exécuté trois fois de suite avec les conditions aux limites suivantes :
La limite de couple de tous les axes est infinie (illimitée).
La limite de couple du bras 2 est réglée sur une valeur inférieure au couple maximal atteint pendant un mouvement illimité. La valeur a été fixée arbitrairement à
2 Nm.La limite de couple du bras 2 est toujours
2 Nm, et en plus une charge a été appliquée au TCP (mLoad=3 kg,lLoad=0.2 m):
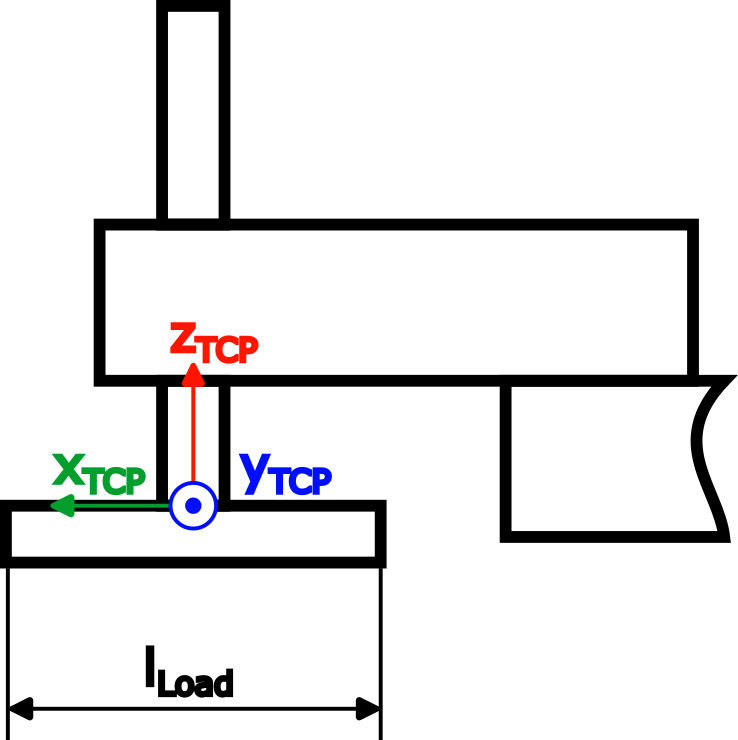 |
Le calcul de l'inertie de la charge a été simplifié grâce à l'utilisation de tiges fines :
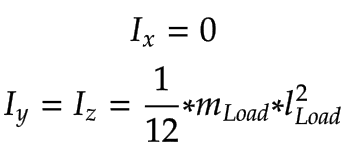 |
Les mouvements peuvent être surveillés dans la trace. Le mouvement 1 a les résultats suivants :
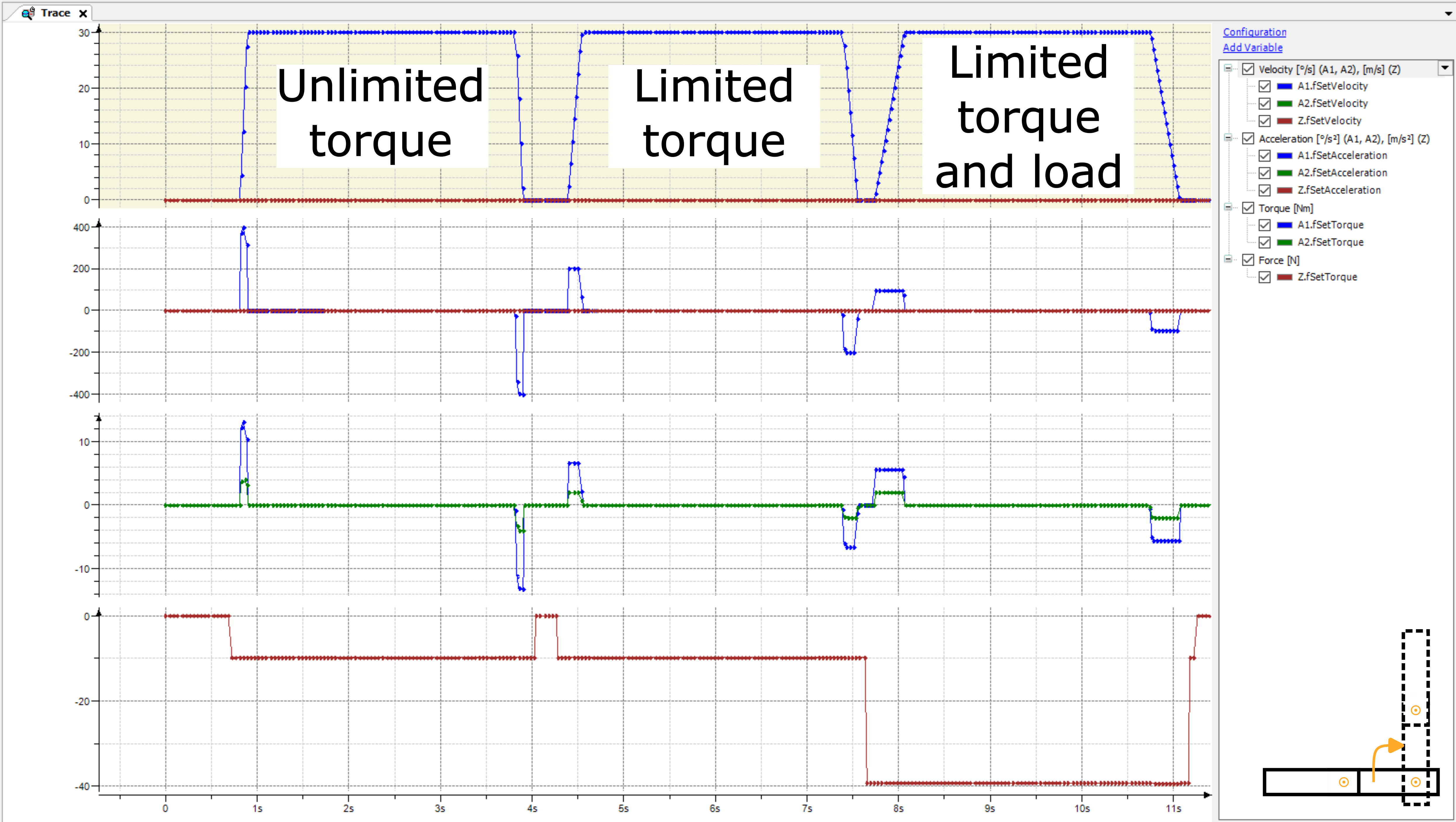
Même si le bras 2 ne bouge pas pendant le mouvement 1, le mouvement du bras 1 entraîne un couple pour le bras 2 pendant l'accélération/la décélération. Le couple calculé est envoyé au variateur et peut potentiellement améliorer la boucle du régulateur en mode régulateur
SMC_velocityouSMC_position. Ceci est également appelé commande anticipatrice de couple.La deuxième exécution avec un couple limité montre que même si le bras 2 ne bouge pas, une limite de couple pour le bras 2 ralentit le mouvement du bras 1. Sans le modèle dynamique, l'accélération et la décélération du bras 1 devraient être réduites manuellement pour cela. mouvement afin d'éviter une contrainte mécanique excessive sur le bras 2.
La troisième course avec une charge ralentit encore plus le mouvement du bras 1 afin de ne pas violer la limite de couple du bras 2.
Les avantages de l'utilisation d'un modèle dynamique sont évidents. Pour éviter des contraintes mécaniques excessives sans modèle dynamique :
Soit les limites dynamiques pour chaque mouvement devraient être définies en fonction de l'état actuel du robot.
Ou les limites dynamiques de tous les axes devraient être réduites de telle manière que tous les mouvements potentiels n'entraîneront pas de contraintes mécaniques excessives sur aucun axe.
La première méthode est une tâche complexe et il peut être difficile de calculer des limites raisonnables, tandis que la seconde méthode entraîne des mouvements qui ne sont pas aussi rapides que possible la plupart du temps. Ces inconvénients n'existent plus avec un modèle dynamique car le robot se déplace toujours le plus vite possible tout en respectant les limites mécaniques de chaque axe.
Ces avantages sont illustrés par les résultats du Mouvement 2 :
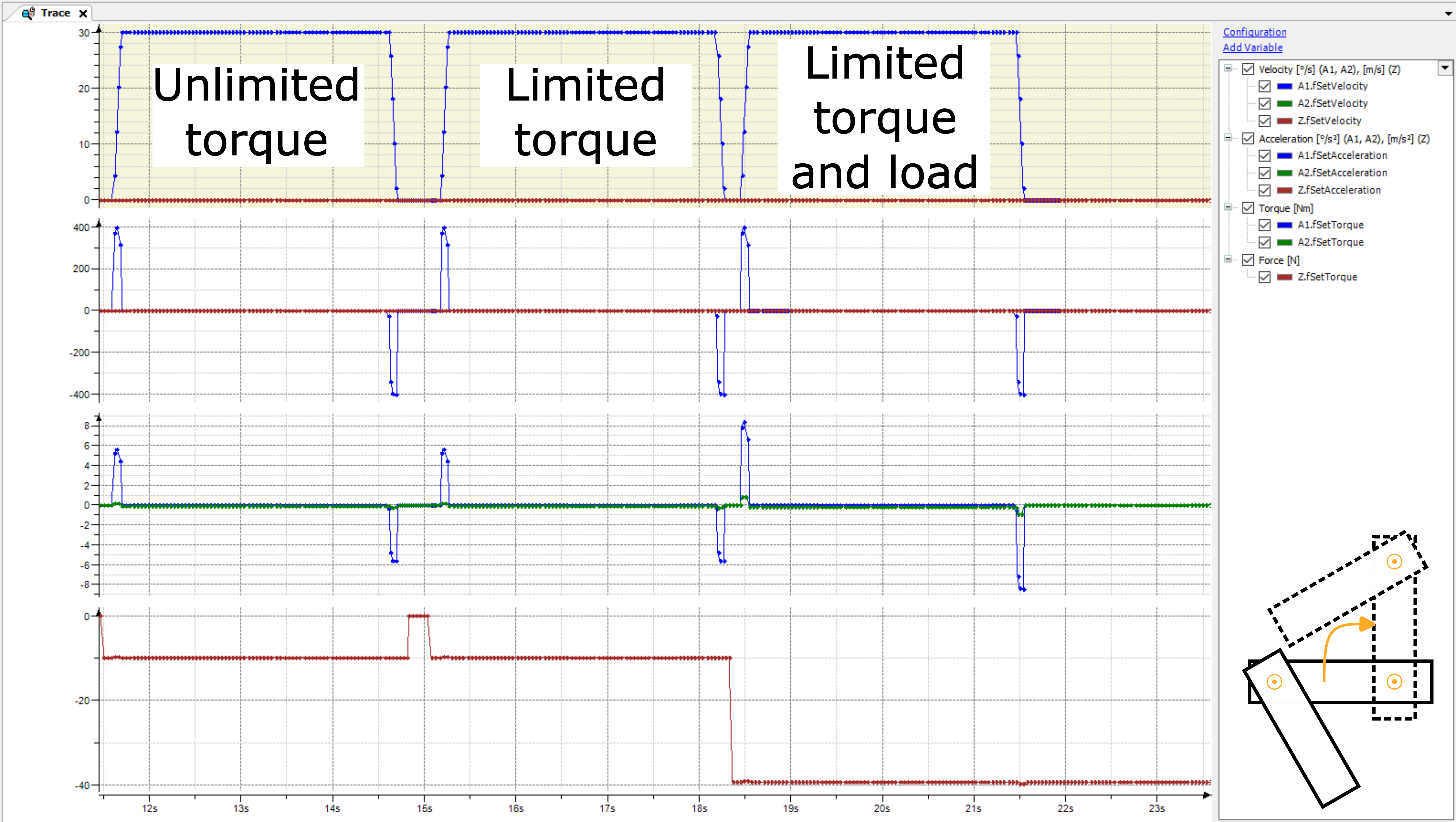
En raison de l'angle du bras 2, le couple résultant du bras 2 est considérablement inférieur à celui du mouvement 1. Par conséquent, les trois courses ne sont jamais limitées par le couple de l'axe. Si l'on avait utilisé des limites dynamiques ajustées basées sur le mouvement 1 (accélération et décélération réduites afin de ne pas violer la limite de couple du bras 2), alors ce mouvement aurait été plus lent que nécessaire.
Partie 2 : Création d'un modèle de robot dynamique
Le modèle qui est créé dans cet exemple est basé sur un algorithme pour les robots à chaîne ouverte tel que présenté dans le livre "Modern Robotics" de KM Lynch et FC Park (voir chapitre 8 "Dynamique des chaînes ouvertes"). L'explication de cet algorithme sort du cadre de cet exemple. Au lieu de cela, l'exemple se concentre sur la façon de définir les valeurs d'entrée de l'algorithme.
Simplifications
Pour rendre cet exemple plus compréhensible, quelques simplifications ont été faites :
Les longueurs de bras
l1etl2(distance entre les axes de rotation) sont utilisées comme longueur de bras totale respective.Le centre de masse est toujours situé au centre géométrique de chaque maillon.
Les matrices d'inertie spatiale des bras et de l'axe Z sont calculées pour des tiges minces.
Exigences du modèle dynamique
Afin d'utiliser le modèle dynamique dans une application SoftMotion, ce modèle doit implémenter le ISMDynamics interface du SM3_Dynamics bibliothèque.
La position zéro, les systèmes de coordonnées et le sens de rotation positif du modèle dynamique peuvent théoriquement s'écarter du modèle cinématique. Cependant, ces différences doivent être prises en considération, et pour simplifier le modèle dynamique, il est donc recommandé d'utiliser les définitions du modèle cinématique.
Étant donné que le modèle dynamique doit calculer les valeurs de couple en Nm et les forces en N, il doit convertir l'unité utilisateur u pour les longueurs en unités SI m. Le facteur de conversion peut être défini par SMC_GroupSetUnits et est inclus dans le addParams entrée de ISMDynamics.AxesStateToTorque. Cet exemple utilise uniquement m pour les longueurs et peut donc ignorer le facteur de conversion.
Spécification des données géométriques et dynamiques du modèle
L'implémentation CEI de l'algorithme présenté dans le livre "Modern Robotics" de KM Lynch et FC Park (voir chapitre 8 "Dynamics of Open Chains") nécessite les valeurs d'entrée suivantes :
La position du centre de masse de chaque maillon lorsque le robot est en position d'origine. La position est spécifiée dans le système de coordonnées du lien précédent (le premier lien est spécifié par rapport au système de coordonnées de base).
La matrice d'inertie spatiale et la masse de chaque lien, exprimées dans le cadre de lien respectif.
L'axe de vis de chaque joint, exprimé dans le cadre de base.
Positions du centre de gravité
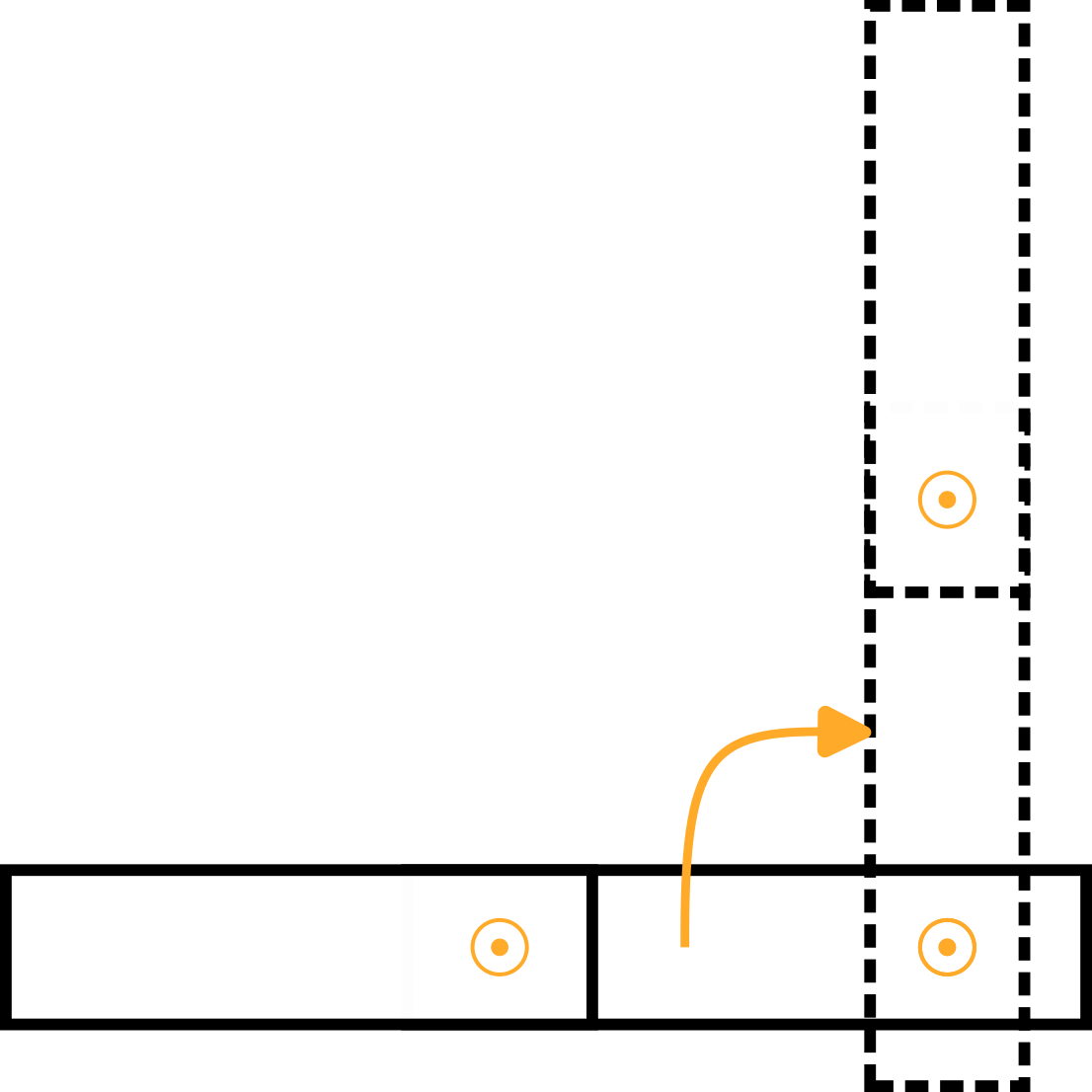
Les cadres avec la position du centre de masse de chaque maillon sont les suivants :
Lien | Cadre | |
|---|---|---|
Bras 1 | Le centre de masse du bras 1, exprimé dans le système de coordonnées de base x0, y0,z0:
Notez qu'il y a une rotation de 180° autour de l'axe x0. | |
Bras 2 | Le centre de masse du bras 2, exprimé dans le système de coordonnées du bras 1 :
| |
Axe z | Le centre de masse de l'axe Z exprimé dans le système de coordonnées du bras 2 :
| |
Point central de l'outil (TCP) | Un cadre supplémentaire pour gérer une charge arbitraire au TCP (par exemple, par un outil, un produit ou une combinaison des deux), exprimée dans le système de coordonnées de l'axe Z :
|
Matrices d'inertie spatiale
Les valeurs d'inertie spatiale doivent être exprimées dans le cadre de liaison respectif. Puisque les cadres sont définis au centre de masse, l'inertie spatiale peut être représentée par une matrice d'inertie de rotation 3x3 et la masse du corps.
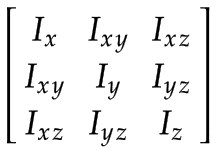 |
Avec la simplification de l'utilisation de tiges minces pour les articulations, les composants de la matrice d'inertie de rotation sont les suivants :
Lien | Matrice d'inertie spatiale | |
|---|---|---|
Bras 1, Bras 2 | Bras 1 et Bras 2 avec leur masse correspondante
| |
Axe z |
|
Axes à vis
Les axes de vis de tous les assemblages doivent être exprimés par rapport au système de coordonnées de base x0, y0,z0.
Lien | Vis Axe | |||
|---|---|---|---|---|
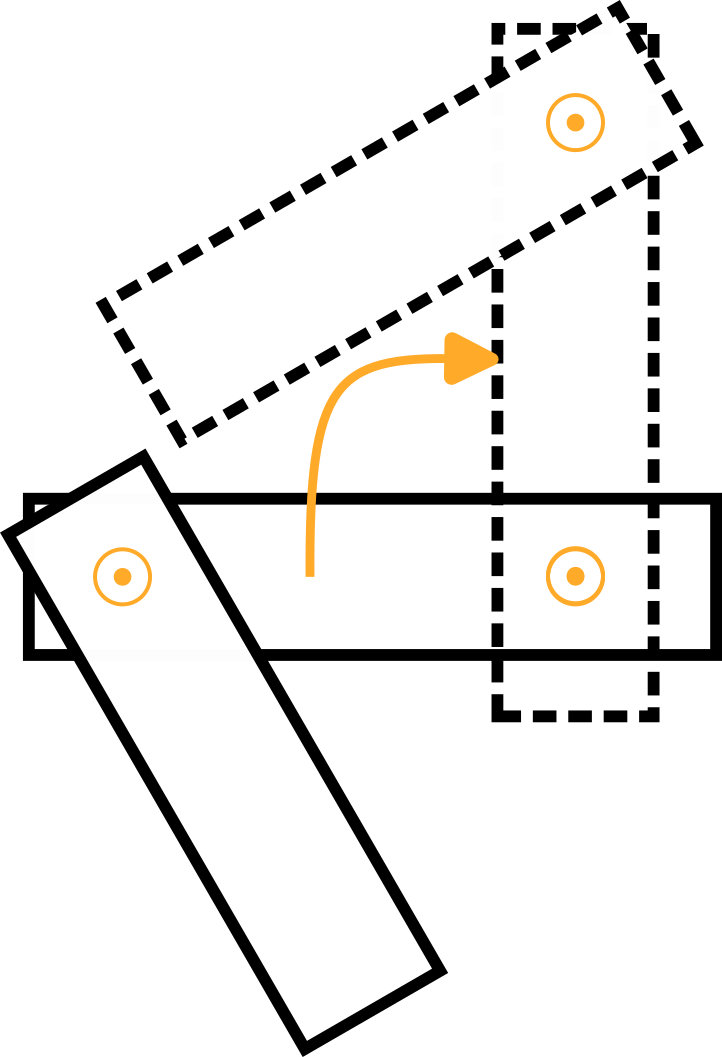
Bras 1 | Imaginez une plaque tournante tournant autour de l'articulation 1 dans le sens positif avec une vitesse angulaire de 1 rad/s. Exprimé dans le système de coordonnées de base, il s'agit d'une rotation positive autour de z0-axe selon la règle de la main droite :
Étant donné que l'axe de rotation du bras 1 est égal au centre du système de coordonnées de base, la vitesse linéaire est nulle : 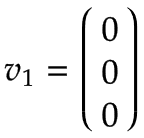 | |||
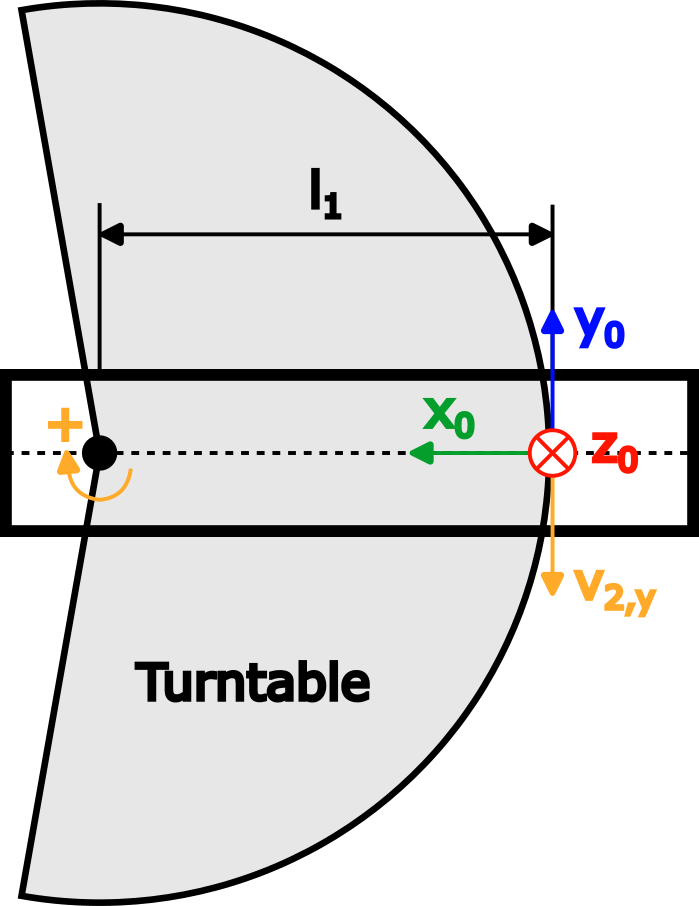
Bras 2 | Encore une fois, imaginez une plaque tournante tournant autour de l'articulation 2 dans le sens positif avec une vitesse angulaire de 1 rad/s, qui est affichée en vue de dessus du bras 1 dans la figure suivante :
Comme pour le bras 1, la vitesse angulaire est :
La figure montre la vitesse linéaire résultante v2,y, qui pointe vers moins y0 direction et est égal à v2,y=-ω2,z * l1.
| |||
Axe z | L'axe Z est un axe prismatique pour lequel les règles suivantes s'appliquent :
Cela conduit aux vecteurs suivants, exprimés dans le système de coordonnées de base x0, y0,z0:
|
Essais
Le modèle dynamique peut maintenant être testé car tous les paramètres du modèle sont définis. Cette section comprend quelques tests de base du modèle.
Vérification des axes de vis
Un axe à vis S avec vitesse angulaire ω et vitesse linéaire v peut être exprimée comme un élément de se(3):
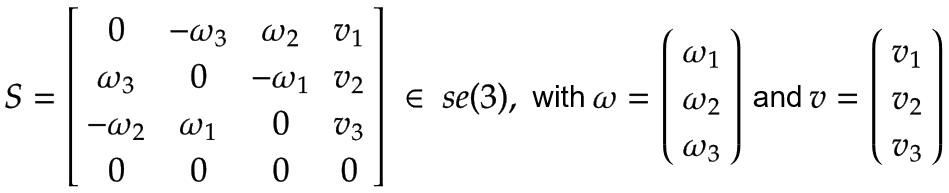 |
Une transformation en avant T peut être exécuté avec les axes à vis S, un cadre effecteur terminal M pour la position zéro du robot, et l'angle d'articulation θ de chaque articulation :
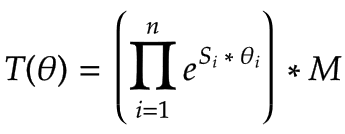 |
L'exemple de projet comprend déjà une fonction qui résout cette équation (voir SMC_OpenChainKinematics_SolveForward). Pour plus de détails, voir le livre "Modern Robotics" de KM Lynch et FC Park.
En utilisant l'équation de transformation directe, on peut maintenant exécuter un test avec des positions d'axe connues et vérifier si la transformation conduit au résultat attendu.
Vérification du calcul du couple à l'arrêt
Pour vérifier les repères de position du centre de masse, vous pouvez calculer manuellement le couple d'axe résultant à l'arrêt pour des positions d'axe données et les comparer aux valeurs calculées par le modèle. Étant donné que cet exemple est basé sur un robot SCARA monté au sol, toutes les positions des axes à l'arrêt conduiront aux mêmes couples ou forces des entraînements :
Découper | Couple/Force résultant |
|---|---|
Bras 1 | Le bras 1 étant un axe de révolution, le résultat est un couple : |
Bras 2 | Le bras 2 étant un axe de révolution, le résultat est un couple : |
Axe z | Comme l'axe Z est un axe prismatique, le résultat est une force : |