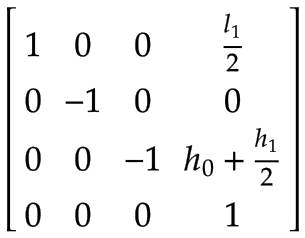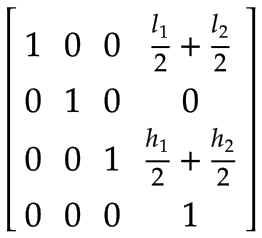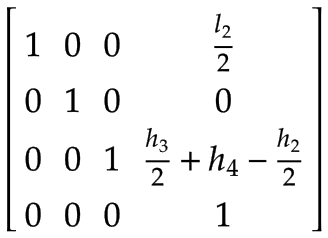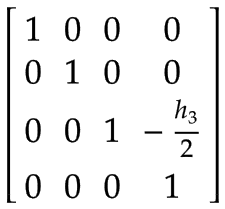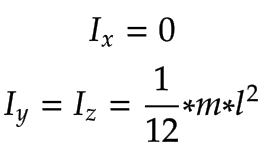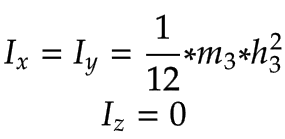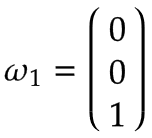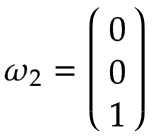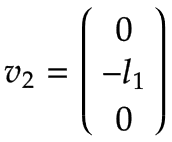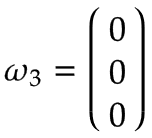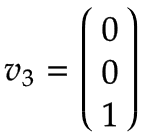Skip to main content

Modelo de robot dinámico

Ver el Robotics_DynamicModel.project proyecto de ejemplo en el directorio de instalación de CODESYS por debajo ..\CODESYS SoftMotion\Examples.

Para limitar los pares/fuerzas del eje durante un movimiento, se requiere un modelo dinámico que calcule estos valores a partir del estado actual del eje (posición, velocidad y aceleración). Este ejemplo incluye las siguientes partes:

  • La parte 1 muestra cómo utilizar un modelo dinámico existente en una aplicación y los resultados de algunos movimientos de muestra.

  • La parte 2 muestra cómo crear un modelo dinámico para un robot SCARA basado en un algoritmo que se presenta en el libro "Modern Robotics" de KM Lynch y FC Park.

Estructura de la aplicación

Parte 1: Uso de un modelo dinámico en una aplicación

  • El código para esta parte se encuentra en el TorqueLimitationDemocarpeta.

  • PLC_PRG es el programa principal, que incluye una máquina de estados que desencadena movimientos de prueba.

  • Los movimientos se pueden controlar mediante el Trace.

Parte 2: Creación de un modelo de robot dinámico

  • El código para el modelo dinámico se encuentra en el DynModel carpeta.

  • DynModel_Scara2_Z es el modelo dinámico del robot SCARA.

  • DynModel_Tests ejecuta todas las pruebas de Test_DynModel_Scara2_Z para comprobar si hay errores comunes.

  • El modelo dinámico se basa en un robot SCARA con dos articulaciones giratorias y un eje Z prismático. A continuación se muestra una figura del robot con las dimensiones y sistemas de coordenadas requeridos para el modelo dinámico:

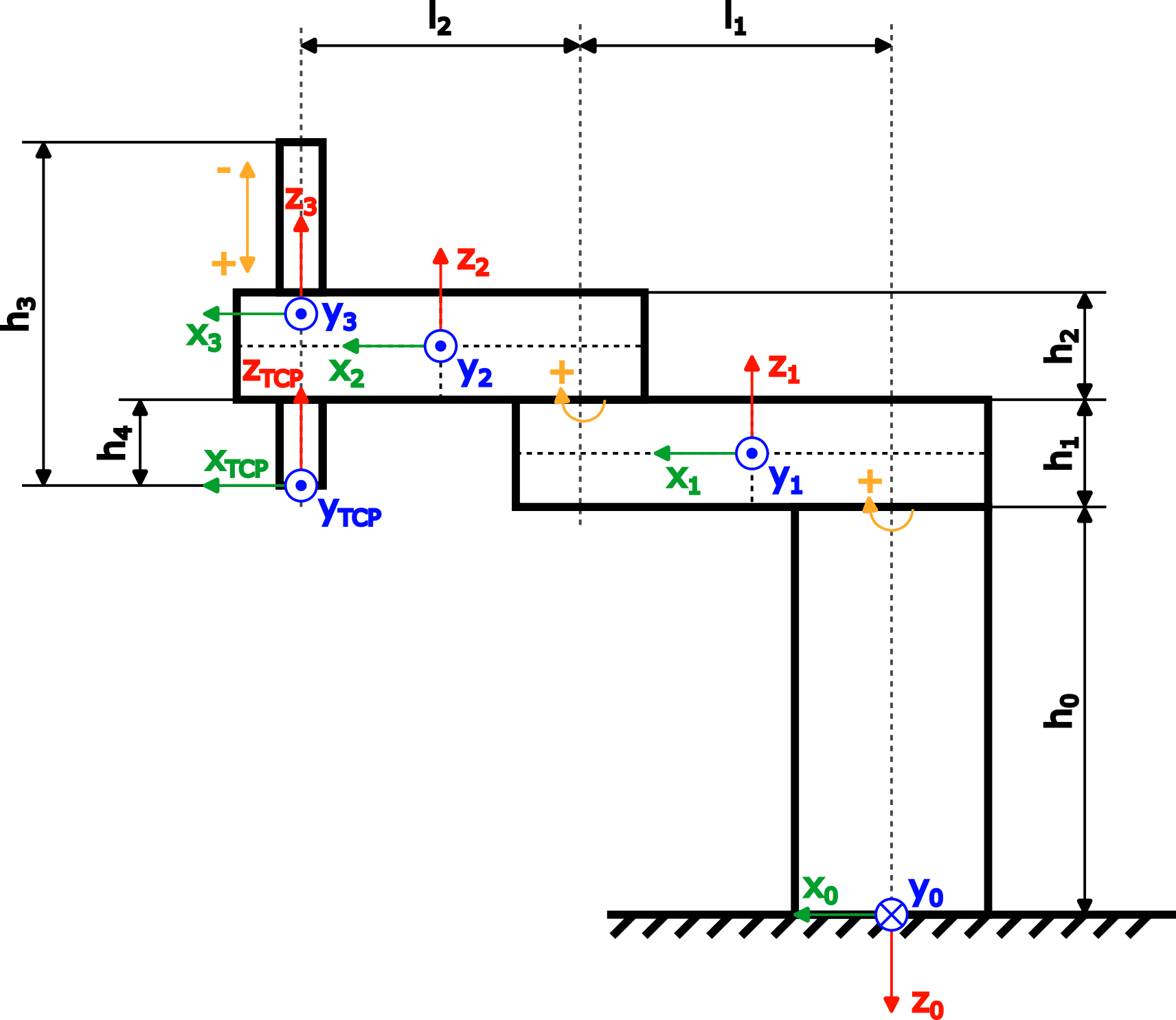
    _sm_img_dynmodel_scara_2_z.png

    Dimensión en la figura

    Nombre de variable correspondiente en el proyecto de muestra en el bloque de funciones DynModel_Scara2_Z

    h0

    baseHeight

    h1

    armOneHeight

    h2

    armTwoHeight

    h3

    zAxisLength

    h4

    zAxisOffset

    l1

    armOneLength

    l1

    armTwoLength

Parte 1: Uso de un modelo dinámico en una aplicación

El uso de un modelo dinámico en una aplicación requiere un modelo que implemente el ISMDynamics interfaz de la SM3_Dynamics biblioteca. El modelo dinámico de Parte 2: Creación de un modelo de robot dinámico se utiliza para esta demostración.

El modelo se puede asignar a un grupo de ejes usando SMC_GroupSetDynamics. Este paso requiere configurar la aceleración gravitacional con respecto al MCS. Debido a que el SCARA en este ejemplo está montado en el piso, la aceleración gravitacional apunta en la dirección z0 positiva. La aceleración gravitatoria debe especificarse en unidades de usuario u/s². Debido a que todas las longitudes en este ejemplo se han definido en la unidad de usuario m, también se debe especificar la aceleración gravitacional en m/s².

SMC_ChangeDynamicLimits se puede utilizar para ajustar los límites de cada eje. Tenga en cuenta que el grupo de ejes debe habilitarse nuevamente usando MC_GroupEnable para activar los nuevos límites dinámicos.

Si se agregan masas adicionales al TCP (por ejemplo, una herramienta o un objeto que es recogido por el robot), entonces SMC_GroupSetLoad se puede utilizar para definir la carga.

los PLC_PRG El programa contiene todos los componentes anteriores y ejecuta dos movimientos de prueba:

Movimiento 1

Movimiento 2

Movimiento del brazo recto de (a0=0°, a1=0°, a2=0 m) a (a0=90°, a1=0°, a2=0,02 m):

_sm_img_dynmodel_one.png

Movimiento del brazo en ángulo de (a0=0°, a1=-120°, a2=0 m) a (a0=90°, a1=-120°, a2=0,02 m):

_sm_img_dynmodel_two.png

Cada movimiento se ejecuta tres veces consecutivas con las siguientes condiciones de contorno:

  • El límite de par de todos los ejes es infinito (ilimitado).

  • El límite de par del Brazo 2 se establece en un valor inferior al par máximo alcanzado durante el movimiento ilimitado. El valor se fijó arbitrariamente en 2 Nm.

  • El límite de torque del brazo 2 todavía está 2 Nm, y además se ha aplicado una carga en el TCP (mLoad=3 kg, lLoad=0.2 m):

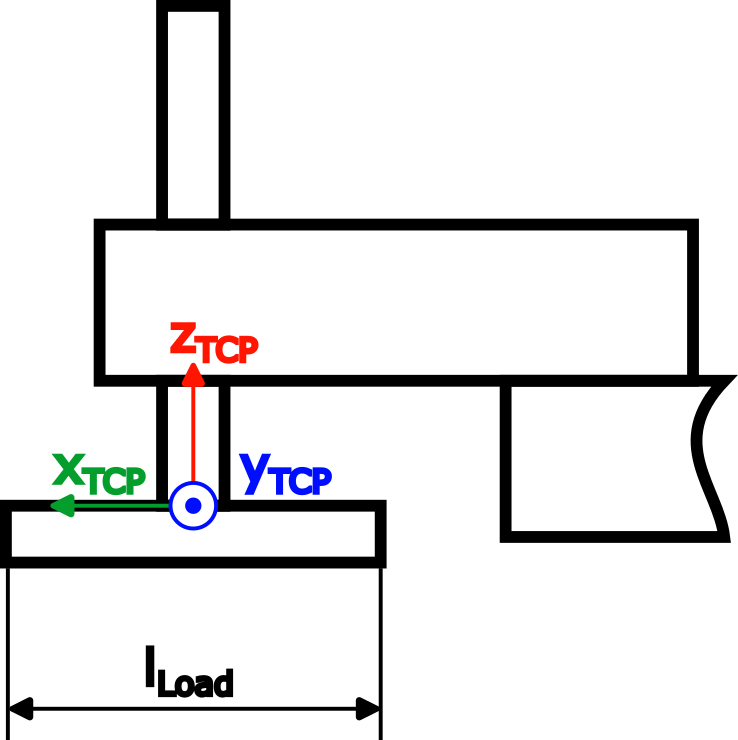_sm_img_robot_with_load.png

El cálculo de la inercia de la carga se ha simplificado utilizando varillas finas:

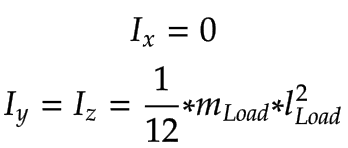_sm_img_load_inertia_tensor.png

Los movimientos pueden ser monitoreados en la traza. El movimiento 1 tiene los siguientes resultados:

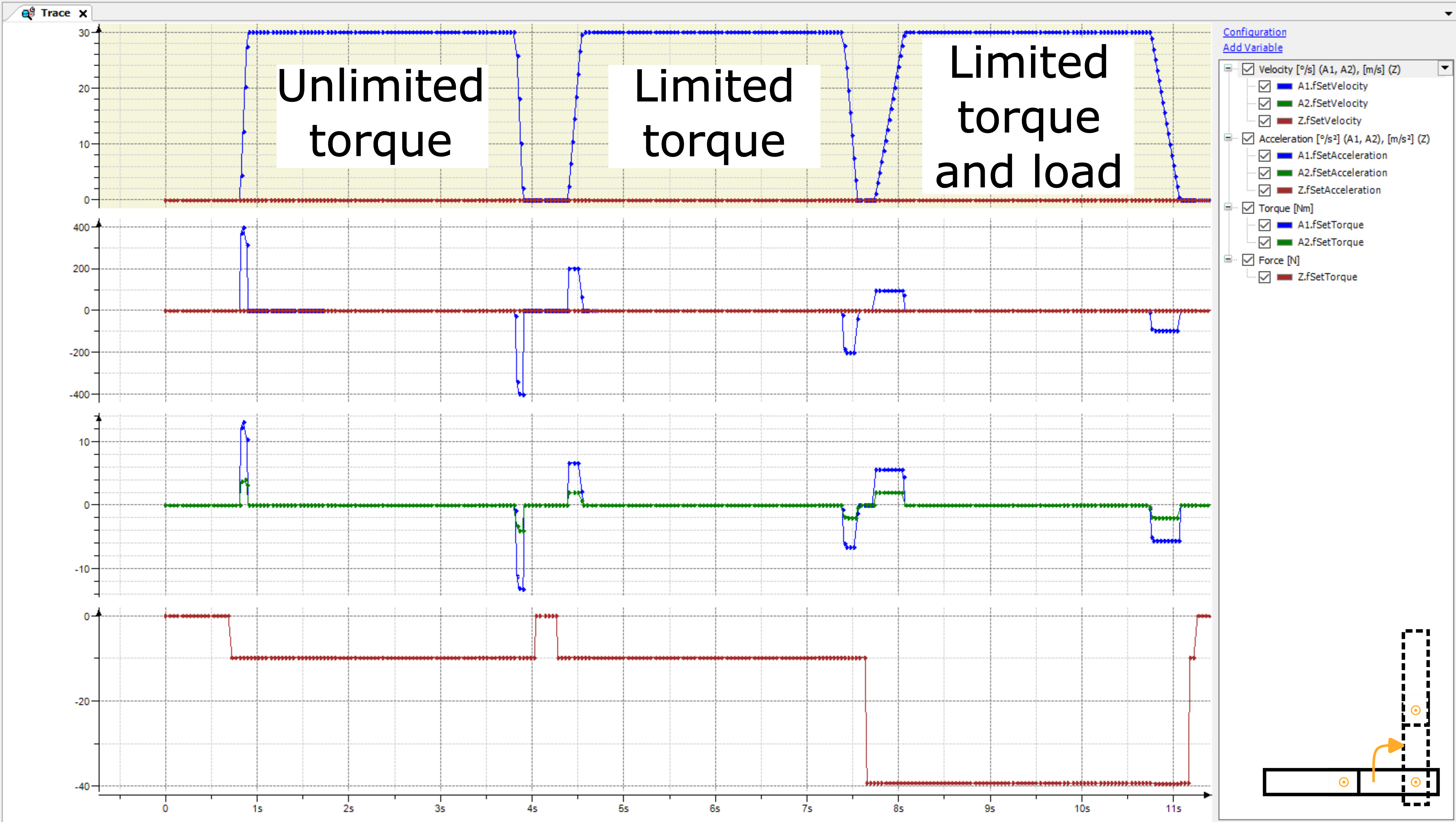
_sm_img_movement_one_results.png

  • Aunque el Brazo 2 no se mueve durante el Movimiento 1, el movimiento del Brazo 1 genera un par para el Brazo 2 durante la aceleración/desaceleración. El par calculado se envía al variador y puede mejorar potencialmente el lazo del controlador en el modo de controlador SMC_velocity o SMC_position. Esto también se denomina control de avance de par.

  • La segunda ejecución con par limitado muestra que aunque el Brazo 2 no se mueva, un límite de par para el Brazo 2 ralentiza el movimiento del Brazo 1. Sin el modelo dinámico, la aceleración y la desaceleración del Brazo 1 tendrían que reducirse manualmente para esto. movimiento para evitar una tensión mecánica excesiva en el Brazo 2.

  • La tercera carrera con carga ralentiza aún más el movimiento del Brazo 1 para no violar el límite de torsión del Brazo 2.

Las ventajas de usar un modelo dinámico son obvias. Para evitar un estrés mecánico excesivo sin un modelo dinámico:

  • Los límites dinámicos para cada movimiento tendrían que establecerse según el estado actual del robot.

  • O los límites dinámicos de todos los ejes tendrían que reducirse de tal manera que todos los movimientos potenciales no conduzcan a una tensión mecánica excesiva en ningún eje.

El primer método es una tarea compleja y puede ser difícil calcular límites razonables, mientras que el segundo método da como resultado movimientos que no son tan rápidos como sea posible la mayor parte del tiempo. Estos inconvenientes ya no existen con un modelo dinámico porque el robot siempre se mueve lo más rápido posible respetando los límites mecánicos de cada eje.

Estas ventajas se ilustran con los resultados del Movimiento 2:

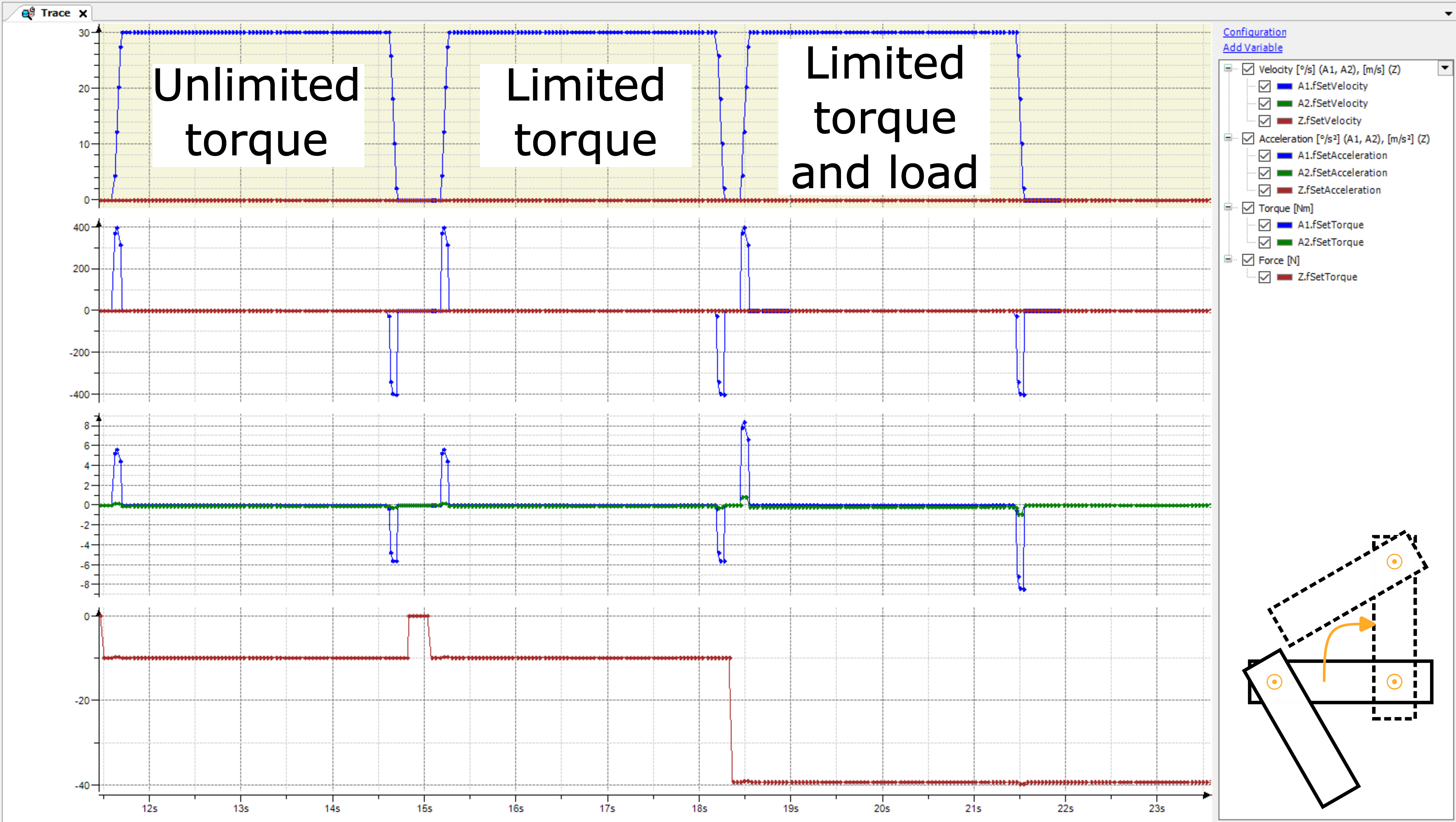
_sm_img_movement_two_results.png

Debido al brazo 2 en ángulo, el par resultante del brazo 2 es considerablemente más bajo que con el movimiento 1. Por lo tanto, las tres carreras nunca están limitadas por el par del eje. Si se hubieran utilizado límites dinámicos ajustados basados en el Movimiento 1 (aceleración y desaceleración reducidas para no violar el límite de torque del Brazo 2), entonces este movimiento habría sido más lento de lo necesario.

Parte 2: Creación de un modelo de robot dinámico

El modelo que se crea en este ejemplo se basa en un algoritmo para robots de cadena abierta como se presenta en el libro "Modern Robotics" de KM Lynch y FC Park (consulte el Capítulo 8 "Dinámica de cadenas abiertas"). La explicación de este algoritmo está más allá del alcance de este ejemplo. En su lugar, el ejemplo se centra en cómo definir los valores de entrada del algoritmo.

simplificaciones

Para hacer este ejemplo más comprensible, se han hecho algunas simplificaciones:

  • Las longitudes de los brazos l1 y l2 (distancia entre los ejes de rotación) se utilizan como su respectiva longitud total del brazo.

  • El centro de masa siempre está ubicado en el centro geométrico de cada eslabón.

  • Las matrices de inercia espacial de los brazos y el eje Z se calculan para varillas delgadas.

Requisitos del modelo dinámico

Para utilizar el modelo dinámico en una aplicación SoftMotion, este modelo tiene que implementar el ISMDynamics interfaz de la SM3_Dynamics biblioteca.

La posición cero, los sistemas de coordenadas y la dirección de rotación positiva del modelo dinámico teóricamente pueden desviarse del modelo cinemático. Sin embargo, estas diferencias deben tenerse en cuenta y, para simplificar el modelo dinámico, se recomienda utilizar las definiciones del modelo cinemático.

Debido a que el modelo dinámico debe calcular los valores de torque en Nm y las fuerzas en N, tiene que convertir la unidad de usuario u para longitudes a unidades SI m. El factor de conversión se puede establecer mediante SMC_GroupSetUnits y está incluido en el addParams entrada de ISMDynamics.AxesStateToTorque. Este ejemplo usa solo m para longitudes y, por lo tanto, puede ignorar el factor de conversión.

Especificación de los datos geométricos y dinámicos del modelo.

La implementación IEC del algoritmo presentado en el libro "Modern Robotics" de KM Lynch y FC Park (consulte el Capítulo 8 "Dinámica de cadenas abiertas") requiere los siguientes valores de entrada:

  • La posición del centro de masa de cada enlace cuando el robot está en la posición inicial. La posición se especifica en el sistema de coordenadas del enlace anterior (el primer enlace se especifica en relación con el sistema de coordenadas base).

  • La matriz de inercia espacial y la masa de cada eslabón, expresadas en el marco de eslabón respectivo.

  • El eje del tornillo de cada junta, expresado en el marco base.

Posiciones del centro de masa

Los cuadros con la posición del centro de masa de cada eslabón son los siguientes:

Enlace

Cuadro

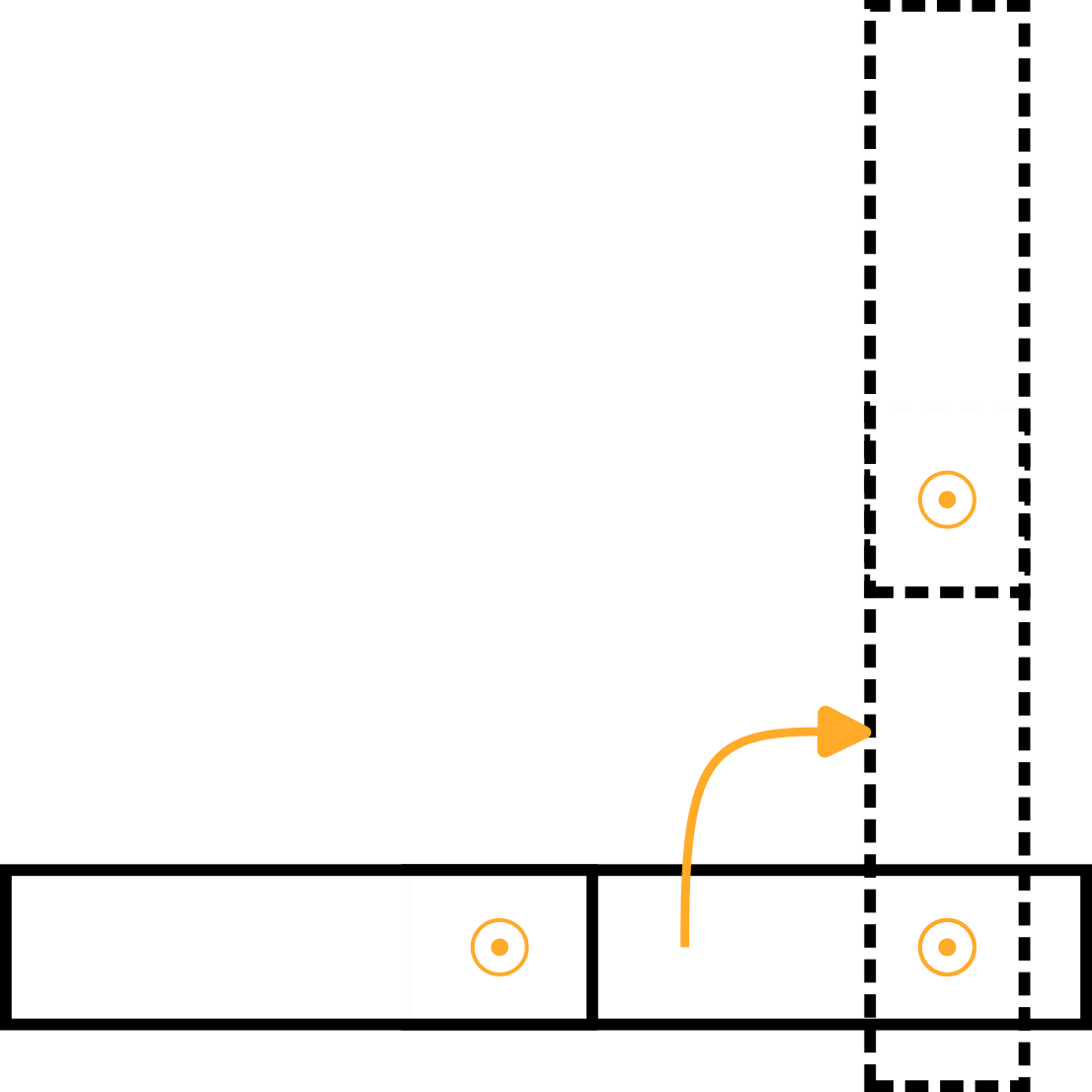
Brazo 1

El centro de masa del Brazo 1, expresado en el sistema de coordenadas base x0, y0, z0:

_sm_img_arm1_centerofmass_frame.png

Tenga en cuenta que hay una rotación de 180° alrededor del eje x0.

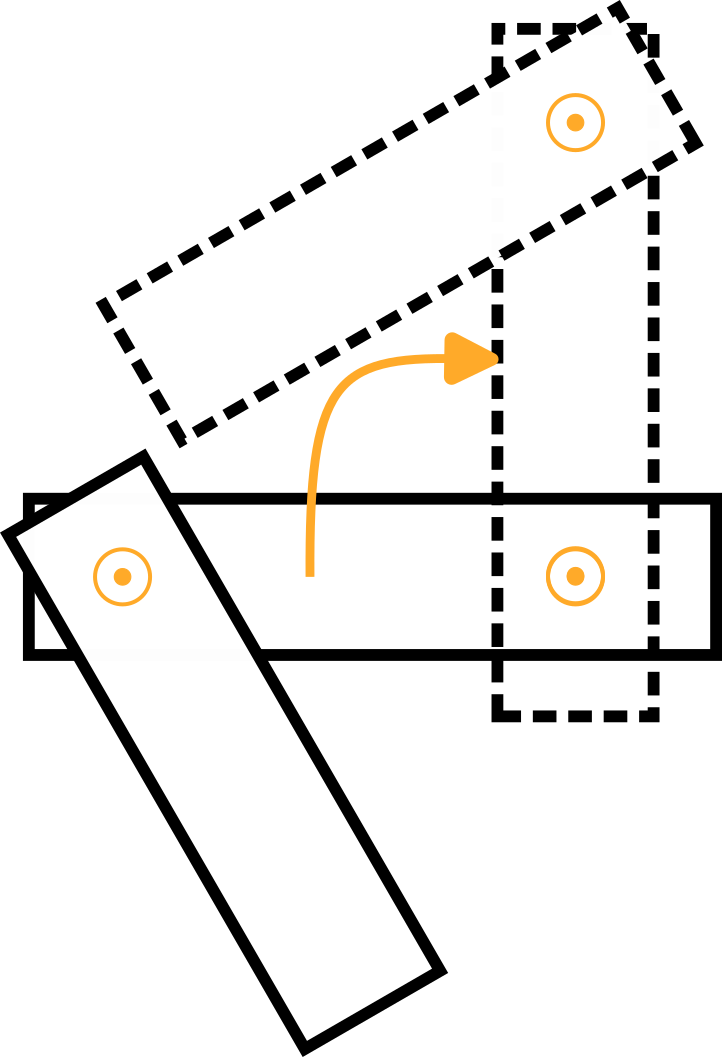
brazo 2

El centro de masa del Brazo 2, expresado en el sistema de coordenadas del Brazo 1:

_sm_img_arm2_centerofmass_frame.png

Eje Z

El centro de masa del eje Z expresado en el sistema de coordenadas del Brazo 2:

_sm_img_zaxis_centerofmass_frame.png

Punto central de la herramienta (TCP)

Un marco adicional para manejar una carga arbitraria en el TCP (por ejemplo, por una herramienta, un producto o una combinación de ambos), expresada en el sistema de coordenadas del eje Z:

_sm_img_externalforce_centerofmass_frame.png

Matrices de inercia espacial

Los valores de inercia espacial deben expresarse en el marco de enlace respectivo. Dado que los marcos están definidos en el centro de masa, la inercia espacial se puede representar mediante una matriz de inercia rotacional de 3x3 y la masa del cuerpo.

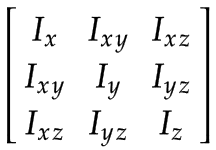_sm_img_general_inertia_tensor.png

Con la simplificación de usar varillas delgadas para las juntas, los componentes de la matriz de inercia rotacional son los siguientes:

Enlace

Matriz de inercia espacial

Brazo 1, Brazo 2

Brazo 1 y Brazo 2 con su masa correspondiente m1 y m2y longitud l1 y l2:

_sm_img_arm1_arm2_inertiatensor.png

Eje Z

_sm_img_zaxis_inertiatensor.png

ejes de tornillo

Los ejes de los tornillos de todas las uniones deben expresarse en relación con el sistema de coordenadas base x0, y0, z0.

Enlace

Eje de tornillo

Brazo 1

Imagine una plataforma giratoria girando alrededor de la articulación 1 en dirección positiva con una velocidad angular de 1 rad/s.

Expresado en el sistema de coordenadas base, esta es una rotación positiva alrededor de la z0-eje según la regla de la mano derecha:

_sm_img_arm1_screwaxis_angularvelocity.png

Debido a que el eje de rotación del Brazo 1 es igual al centro del sistema de coordenadas base, la velocidad lineal es cero: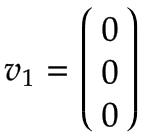

_sm_arm1_screwaxis_linearvelocity.png

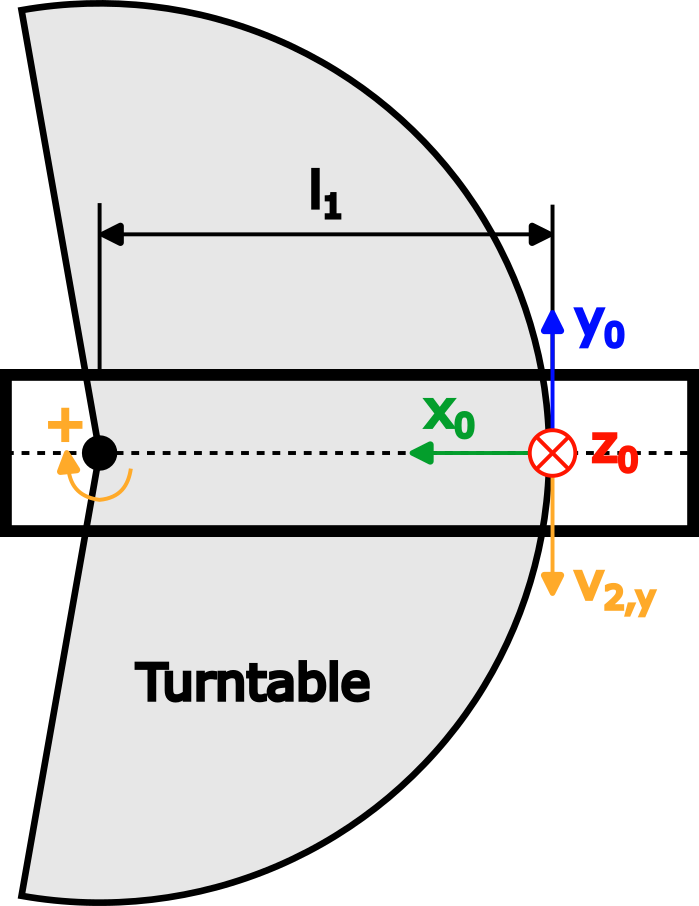
brazo 2

Nuevamente, imagine una plataforma giratoria girando alrededor de la articulación 2 en dirección positiva con una velocidad angular de 1 rad/s, que se muestra en la vista superior del brazo 1 en la siguiente figura:

_sm_img_arm2_screwaxis.png

En cuanto al Brazo 1, la velocidad angular es:

_sm_img_arm2_screwaxis_angularvelocity.png

La figura muestra la velocidad lineal resultante v2 años, que apunta en y negativa0 dirección y es igual a v2 años=-ω2,z * yo1.

_sm_img_arm2_screwaxis_linearvelocity.png

Eje Z

El eje Z es un eje prismático para el que se aplican las siguientes reglas:

  • El vector de velocidad angular ω es cero.

  • El vector de velocidad lineal es un vector unitario en la dirección de traslación positiva.

Esto conduce a los siguientes vectores, expresados en el sistema de coordenadas base x0, y0, z0:

_sm_img_zaxis_screwaxis_angularvelocity.png
_sm_img_zaxis_screwaxis_linearvelocity.png

Pruebas

Ahora se puede probar el modelo dinámico porque todos los parámetros del modelo están definidos. Esta sección incluye algunas pruebas básicas del modelo.

Comprobación de los ejes de los tornillos

Un eje de tornillo S con velocidad angular ω y velocidad lineal v puede expresarse como un elemento de se(3):

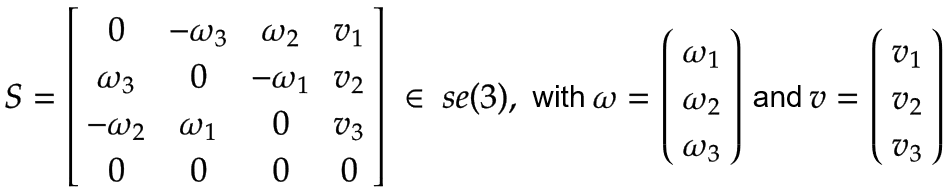_sm_img_screwaxis_se3.png

Una transformación hacia adelante T se puede ejecutar con los ejes de tornillo S, un marco de efector final M para la posición cero del robot y el ángulo de articulación θ de cada articulación:

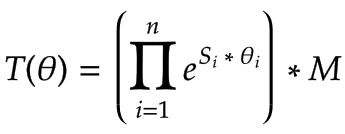_sm_img_screwaxis_forwardtransformation.png

El proyecto de muestra ya incluye una función que resuelve esta ecuación (ver SMC_OpenChainKinematics_SolveForward). Para más detalles, consulte el libro "Modern Robotics" de KM Lynch y FC Park.

Usando la ecuación de transformación directa, ahora se puede ejecutar una prueba con posiciones de eje conocidas y verificar si la transformación conduce al resultado esperado.

Comprobación del cálculo del par en parada

Para verificar los marcos de posición del centro de masa, se puede calcular manualmente el par de eje resultante en reposo para posiciones de eje dadas y compararlos con los valores calculados por el modelo. Dado que este ejemplo se basa en un robot SCARA montado en el suelo, todas las posiciones de los ejes en reposo darán lugar a los mismos pares o fuerzas de los accionamientos:

Articulación

Par/fuerza resultante

Brazo 1

Como el brazo 1 es un eje de revolución, el resultado es un par: M1=0 Nm.

brazo 2

Como el brazo 2 es un eje de revolución, el resultado es un par: M2=0 Nm.

Eje Z

Como el eje Z es un eje prismático, el resultado es una fuerza: F3=m3*g Ncon aceleración gravitatoria g.

En esta sección: