Metrics
Detailed description of metrics provided by CODESYS Static Analysis
Tip
The Code size, Variable size, Stack size, and Number of calls metrics are reported only for POUs from libraries which are integrated in the project.
Metric: Code size (number of bytes)
Categories: Informative, Efficiency
Number of bytes which a function block contributes to the application code
The number also depends on the code generator. For example, the code generator for ARM processors generally generates more bytes than the code generator for x86 processors.
Metric: Variable size (number of bytes)
Categories: Informative, Efficiency
Size of the static memory which is used by the object
For function blocks, this is the size which is used for an instance of the function block (which may include memory gaps, depending on the memory alignment). For programs, functions, and global variable lists, this is the sum of the size of all static variables.
Example
FUNCTION FUN1 : INT
VAR_INPUT
a,b : INT;
END_VAR
VAR
c,d : INT;
END_VAR
VAR_STAT
f,g,h : INT;
END_VARThe function has 3 static variables of type INT (f, g, and h), each of which requires 2 bytes of memory. As a result, FUN1 has a variable size of 6 bytes.
Metric: Stack size (number of bytes)
Categories: Informative, Efficiency, Reliability
Number of bytes which are required for calling a function or a function block
Input variables and output variables are aligned to the memory. This can create a gap between these variables and the local variables. This gap is counted.
Return values of called functions which do not fit into a register, are pushed onto the stack. The largest of these values determines the additional allocated memory, which also counts. Functions or function blocks which are called within the POUs under consideration have their own stack frame. Therefore, the memory for such calls does not count.
Depending on the code generator used, intermediate results of calculations also use the stack. These results are not counted.
//Declaration
FUNCTION FUN1 : INT
VAR_INPUT
a,b : INT;
END_VAR
VAR
c,d,e : INT;
END_VAR
VAR_STAT
f,g,h : INT;
END_VAR
//Implementation
c := b;
d := a;
e := a+b;Assumption: For the calculation, assume a CODESYS Control Win which uses the x86 code generator.
The above example has a caller size of 8 bytes: 4 bytes for the two INT inputs and 4 bytes for the return value. The device has a stack alignment of 4 bytes, so that there is a gap of 2 bytes. The caller size is 8 bytes: three local variables with 2 bytes each plus the 2 byte gap for stack alignment. As a result, the total stack size of FUN1 is 16 bytes.
VAR_STAT is not stored on the stack and therefore does not increase the stack size of a POU.
Metric: Number of calls (Calls)
Category: Informative
Number of calls of the POU under Program unit
//Declaration PLC_PRG
PROGRAM PLC_PRG
VAR
myFB : FB1;
END_VAR
//Implementation
myFB(b := FALSE);//Declaration FB1
FUNCTION_BLOCK FB1
VAR_INPUT
b : BOOL;
END_VAR
VAR
i : INT;
END_VAR
//Implementation
METH(i);
IF b THEN
METH(i*i);
END_IF
//Declaration FB1.METH
METHOD METH : BOOL
VAR_INPUT
i : INT;
END_VAR
//Implementation
METH := i >= 42;If PLC_PRG is called in a task, then this call is also counted.
FB1 has exactly one call (in PLC_PRG).
METH has two calls, both in FB1.
Metric: Number of calls from tasks (Tasks)
Categories: Maintainability, Reliability
Number of tasks (Tasks) where the POU specified under Program unit is called
In the case of function blocks, the number of tasks is counted, in which the function block itself or any function block in the inheritance tree of the function block is called.
In the case of methods and actions, the number of tasks is displayed, in which the (parent) function block is called.
FUNCTION_BLOCK FB //...
FUNCTION_BLOCK FB2 EXTENDS FB //...
FUNCTION_BLOCK FB3 EXTENDS FB2 //...
Each function block is called in its own PROGRAM. Each PROGRAM has its own task.
The Called in tasks metric returns in 1 for FB3 and 2 for FB2 because the calls from FB3 and FB2 are counted. The metric results in 3 for FB because in this case the calls from FB3, FB2, and FB are counted.
Metric: Number of global variables used (Globals)
Categories: Maintainability, Reusability
Number of used global variables in the POU under Program unit
//GVL
VAR_GLOBAL
gvla : INT;
gvlb : INT;
gvlc : INT;
END_VAR/PRG declaration
PROGRAM PRG
VAR
x : INT := GVL.gvlc;
y : INT;
END_VAR
//PRG implementation
x := GVL.gvla;
y := GVL.gvla*GVL.gvlb;The PRG program uses 3 variables from GVL: gvla, gvlb, and gvlc.
Metric: Number of direct address accesses (IOs)
Categories: Reusability, Maintainability
Number of direct address accesses (IOs) in the implementation of the object.
//Declaration
PROGRAM PRG
VAR
xVar : BOOL:= %IX0.0; // +1 direct address access
byVar : BYTE;
END_VAR
//Implementation
xVar := %IX0.0; // +1 direct address access
%QX0.0 := xVar; // +1
%MX0.1 := xVar; // +1
%MB1 := byVar; // +1The example has 5 direct address accesses.
Metric: Number of local variables (Locals)
Categories: Informative, Efficiency
Number of variables declared in the VAR area of the POU. Inherited variables are not counted.
//Declaration
FUNCTION_BLOCK FB
VAR_INPUT
END_VAR
VAR_OUTPUT
END_VAR
VAR
i,j,k,l : INT;
m,n,o : BOOL;
END_VAR
In the function block, 7 local variables are declared.
Metric: Number of input variables (Inputs)
Categories: Maintainability, Reusability
Default upper limit for the corresponding SA0166 rule: 10
Number of variables declared in VAR_INPUT of the program unit. Inherited input variables are not counted.
FUNCTION_BLOCK FB
VAR_INPUT
i : INT;
r : REAL;
END_VAR
In the function block, 2 input variables are declared: i and r.
METHOD METH : BOOL
VAR_INPUT
j : INT;
l : LREAL;
END_VAR
The method has 2 inputs: j and l
Metric: Number of output variables (Outputs)
Categories: Maintainability, Reusability
Default upper limit for the corresponding SA0166 rule: 10
Number of variables in VAR_OUTPUT of the program unit
In the case of function blocks, this is the number of custom output variables (VAR_OUTPUT). In the case of methods and functions, this is the number of custom output variables plus one if they have a return value. The return value is also counted. Inherited output variables are not counted.
A high number of output variables is an indication of a violation of the principle of unique responsibility.
FUNCTION_BLOCK FB
VAR_OUTPUT
i : INT; // +1 output
r : REAL; // +1 output
END_VARThe function block has 2 output variables: i and r
METHOD METH : BOOL
VAR_INPUT
j : INT;
l : LREAL;
END_VARThe method has 3 outputs: METH, j, and l
METHOD METH1 // +0 outputs (no return type)
VAR_OUTPUT
ar : ARRAY[0..10] OF INT; // +1 output
l : LREAL; // +1 output
END_VARThe METH1 method has 2 outputs: ar and i
Metric: NOS – Number Of Statements
Category: Informative
Number of statements in the implementation of a function block, function, or method
Statements in the declaration, empty statements, or pragmas are not counted.
//Declaration:
FUNCTION POU : BOOL
VAR_INPUT
END_VAR
VAR
c : INT := 100; // statements in the declaration are not counted
END_VAR
VAR_OUTPUT
test : INT;
i : INT;
END_VAR
//Implementation:
IF TRUE THEN //if statement: +1
test := 0; // +1
END_IF
WHILE test = 1 DO //while statement: +1
; // empty statements do not add to the statement count
END_WHILE
FOR c := 0 TO 10 BY 2 DO //for statement: +1
i := i+i; // +1
END_FOR
{text 'simple text pragma'} //pragmas are not counted
test := 2; //+1The example has 6 statements.
Metric: Percentage of comment
Category: Maintainability
Percentage of comments in source code
This number is calculated according to the following formula:
Percentage = 100 * <characters in comments> / <sum of characters in source code and characters in comments>
Multiple consecutive spaces in the source code are counted as one space, which prevents high weighting of indented source code. For empty objects (no source code and no comments), a percentage of 0 is returned.
Declaration part:
FUNCTION_BLOCK FB //comments in the declaration are counted, as well
VAR_TEMP
hugo : INT;
END_VARImplementation:
hugo := hugo + 1; //Declaration: 40 letters non comment; 50 letters comment //Implementation: 13 letters non comment; 152 letters comment // 100 * 202 / 255 -> 79% comments
The calculation of the percentage 100 * 202 / 255 returns 79%.
Metric: Complexity (McCabe)
Category: Testability
Recommended upper limit: 10
The cyclomatic complexity according to McCabe is a measure of the readability and testability of source code. It is calculated by counting the number of binary branches in the control flow of the POU. However, cyclomatic complexity penalizes high branching because high branching increases the number of test cases required for high test coverage.
IF statement// every POU has an initial cyclomatic complexity of 1, since it has at least 1 branch
IF b1 THEN // +1 for the THEN branch
;
ELSIF b2 THEN // +1 for the THEN branch of the IF inside the else
;
ELSE
IF b3 OR b4 THEN // +1 for the THEN branch
;
END_IF
END_IFThe code snippet has a cyclomatic complexity of 4.
CASE statement// every POU has an initial cyclomatic complexity of 1, since it has at least 1 branch
CASE a OF
1: ; // +1
2: ; // +1
3,4,5: ; // +1
ELSE // the ELSE statement does not increase the cyclomatic complexity
;
END_CASEThe code snippet has a cyclomatic complexity of 4.
// every POU has an initial cyclomatic complexity of 1, since it has at least 1 branch
WHILE b1 DO // +1 for the WHILE loop
;
END_WHILE
REPEAT // +1 for the REPEAT loop
;
UNTIL b2
END_REPEAT
FOR a := 0 TO 100 BY 2 DO // +1 for the REPEAT loop
;
END_FORThe code snippet has a cyclomatic complexity of 4.
The following statements also increase the cyclomatic complexity:
//Declaration
FUNCTION FUN : STRING
VAR_INPUT
condition_return : BOOL;
condition_jmp : BOOL;
END_VAR
VAR
END_VAR
//Implementation
// every POU has an initial cyclomatic complexity of 1, since it has at least 1 branch
JMP(condition_jmp) lbl; //Conditional jumps increase the cyclomatic complexity by 1
FUN := 'u';
RETURN(condition_return); //Conditional returns increase the cyclomatic complexity by 1, too
lbl:
FUN := 't';
The code snippet has a cyclomatic complexity of 3.
Metric: Cognitive Complexity
Category: Maintainability
Default upper limit for the corresponding SA0178 rule: 20
Cognitive complexity is a measure of the readability and understandability of source code as introduced by Sonarsource™ in 2016. However, it penalizes heavy nesting of the control flow and complex Boolean expressions. Cognitive complexity is calculated only for structured text implementations.
The following examples show how cognitive complexity is calculated.
Tip
The Show Cognitive Complexity for Current Editor command can be used to additionally display the increments for structured text.
Statements which manipulate control flow increase the cognitive complexity by 1
IF TRUE THEN // +1 cognitive complexity
;
END_IF
WHILE TRUE DO //+1 cognitive complexity
;
END_WHILE
FOR i := 0 TO 10 BY 1 DO //+1 cognitive complexity
;
END_FOR
REPEAT //+1 cognitive complexity
;
UNTIL TRUE
END_REPEATThe code snippet has a cognitive complexity of 4.
When nesting the control flow, an increment of 1 is added for each level of nesting.
IF TRUE THEN //+1 cognitive complexity
WHILE TRUE DO //+2 (+1 for the loop itself, +1 for the nesting inside the IF)
FOR i := 0 TO 10 BY 1 DO //+3 (+1 for the FOR loop itself, +2 for the nesting inside the WHILE and the IF)
;
END_FOR
END_WHILE
REPEAT //+2 (+1 for the loop itself, +1 for the nesting inside the IF)
;
UNTIL TRUE
END_REPEAT
END_IFThe code snippet has a cognitive complexity of 8.
Because Boolean expressions play a major role in understanding source code, they are also taken into account when calculating cognitive complexity.
Understanding Boolean expressions which are associated with the same Boolean operator is not as difficult as understanding a Boolean expression which contains alternating Boolean operators. Therefore, any chain of identical Boolean operators in an expression increases cognitive complexity.
b := b1; //+0: a simple expression, containing no operators, has no increment
The simple expression without an operator has an increment of 0.
b := b1 AND b2; //+1: one chain of AND operators
The expression with an AND link has an increment of 1.
b := b1 AND b2 AND b3; //+1: one more AND, but the number of chains of operators does not change
The expression has one more AND. But since it is the same operator, the number of the chain formed with identical operators does not change.
b := b1 AND b2 OR b3; //+2: one chain of AND operators and one chain of OR operators
The expression has a chain of AND operators and a chain of OR operators. This results in an increment of 2.
b := b1 AND b2 OR b3 AND b4 AND b5; //+3
The code snippet has an increment of 3.
b := b1 AND NOT b2 AND b3; //+1: the unary NOT operator is not considered in the cognitive complexity
The unary operator NOT is not considered in cognitive complexity.
Structured text has additional statements and expressions which change the control flow.
The following statements are penalized with an increment of cognitive complexity:
aNewLabel: x := MUX(i, a,b,c); //+1 for MUX operator y := SEL(b, i,j); //+1 for SEL operator JMP aNewLabel; //+1 for JMP to label
EXIT and RETURN statements do not increase cognitive complexity.
Metric: DIT – Depth of Inheritance Tree
Category: Maintainability
Number of inheritances until a function block is reached which does not extend any other function block
FUNCTION_BLOCK MyBaseFB // ... FUNCTION_BLOCK AChildFB EXTENDS MyBaseFB // ... FUNCTION_BLOCK AGrandChildFB EXTENDS AChildFB // ...
MyBaseFB has a DIT of 0 because it is itself a function block which does not extend any other function block.
For AChildFB, the DIT is 1 because one step is required to get to MyBaseFB.
AGrandChildFB has a DIT of 2: One step is needed to AChildFB and another to MyBaseFB.
Metric: NOC – Number Of Children
Categories: Reusability, Maintainability
Number of function blocks which extend the given basic function block. Function blocks which indirectly extend a basic function block are not counted.
FUNCTION_BLOCK MyBaseFB // ... FUNCTION_BLOCK AChildFB EXTENDS MyBaseFB // ... FUNCTION_BLOCK AGrandChildFB EXTENDS AChildFB // ...
MyBaseFB has only one (1) child object: AChildFB, which in turn has the one child object, AGrandChildFB. AGrandChildFB has no child objects.
Metrics: RFC – Response For class
Categories: Maintainability, Reusability
Number of different POUs, methods, or actions which are called and therefore generate a response of the POU specified under Program unit
//Declaration FB1
FUNCTION_BLOCK FB1
VAR
d,x,y : INT;
END_VAR
//Implementation
x := METH(d+10);
y := FUN(42, 0.815);//Declaration FB1.METH
METHOD METH : INT
VAR_INPUT
i : INT;
END_VAR
//Implementation
METH := FUN(CUBE(i), 3.1415);//Declaration CUBE
FUNCTION CUBE : INT
VAR_INPUT
i : INT;
END_VAR
//Implementation
CUBE := i*i*i;//Declaration Function FUN
FUNCTION FUN : INT
VAR_INPUT
a : INT;
lr : LREAL;
END_VAR
//Implementation
FUN := LREAL_TO_INT(lr*10)*a;Starting with
FUNandCUBE, these functions have an RFC of 0 because none of them call other functions, function blocks, or methods for their calculations.FB1.METHusesFUNandCUBE, which results in an RFC of 2.The function block
FB1itself callsMETHandFUN, which increases its RFC by 2.For FB1, its METH method also has to be taken into account. METH uses FUN and CUBE. FUN has already been added to the RFC. Therefore, only the use of CUBE in METH increases the RFC for FB1 to 3
Metric: CBO – Coupling Between Objects
Categories: Maintainability, Reusability
Default upper limit for the corresponding SA0179 rule: 30
Number of other function blocks which are instantiated and used in a function block
A function block with a high coupling between objects is likely to be involved in many different tasks and therefore violates the principle of unique responsibility.
// Declaration
FUNCTION_BLOCK FB_Child EXTENDS FB_Base objects // +0 for EXTENDS
VAR_INPUT
END_VAR
VAR_OUTPUT
END_VAR
VAR
i_fb1 : FB1; // +1 instantiated here
i_fb2 : FB2; // +1 instantiated here
END_VAR
//Implementation
i_fb3(); // +0 instantiated in FB_Base, no increment for callThe extension of a function block does not increase the coupling between objects.
i_fb3is instantiated in the implementation ofFB_Baseand passed on to FB_Child (EXTENDS). The call inFB_Childdoes not increase the coupling between the objects.The CBO of
FB_Childis 2.
Metric: Complexity of reference (Elshof)
Categories: Efficiency, Maintainability, Reusability
Complexity of the data flow of a POU
The referencing complexity is calculated according to the following formula:
<number of variables used> / <number of variable accesses>
Only variable accesses in the implementation part of the POU are considered.
//Declaration
PROGRAM PRG
VAR
i, j : INT;
k : INT := GVL.m;
b, c : BOOL;
myFB : FB;
END_VAR
//Implementation
myFB(paramA := b); // +3 accesses (myFB, paramA and b)
i := j; // +2 accesses (i and j)
j := GVL.d; // +2 accesses (j and GVL.d)Referencing complexity in the code snippet results:
6 number of variables used / 7 number of variable accesses = 0.85
Caution:
candkare not used and therefore do not count as "variables used".The assignment
k : INT := GVL.mis not counted because it is part of the declaration of the program.
Metric: Lack of Cohesion Of Methods – LCOM
Lack of Cohesion Of Methods – LCOM
Categories: Maintainability, Reusability
The cohesion between function blocks, their actions, transitions, and methods describes whether or not they access the same variables.
The lack of cohesion of methods describes how strongly the objects of a function block are connected to each other. The lower the lack of cohesion, the stronger the connection between the objects.
Function blocks with a high lack of cohesion are likely to be involved in many different tasks and therefore violate the principle of unique responsibility.
The metric is calculated according to the following formula:
MAX(0, <number of object pairs without cohesion> - <number of object pairs with cohesion>)
//Declaration
FUNCTION_BLOCK FB
VAR_INPUT
a : BOOL;
END_VAR
VAR_OUTPUT
END_VAR
VAR
i,b : BOOL;
END_VAR
//Implementation
i := 42;
//FB.ACT
i:= 0;//FB.METH Declaration METHOD METH : BOOL VAR_INPUT c : BOOL; END_VAR //Implementation METH := c; i := 1;
//FB.SecondMETH Declaration METHOD SecondMETH : INT VAR_INPUT END_VAR //Implementation SecondMETH := SEL(c,3,4);
Object pairs without connection (4 pairs):
FB,FB.ACTFB,FB.METHFB.ACT,FB.SecondMETHFB.METH,FB.SecondMETH
Object pairs with connection (2 pairs):
FB,FB.SecondMETH(both usec)FB.ACT,FB.METH(both usei)
FB |
|
|
| |
|---|---|---|---|---|
|
| 0 | 0 | . |
| 0 |
| . | . |
| 0 | . | . | . |
| - | . | . | . |
Metric: Number of SFC branches
Categories: Testability, Maintainability
Number of alternative and parallel branches of a POU of the SFC (sequential function chart) implementation language
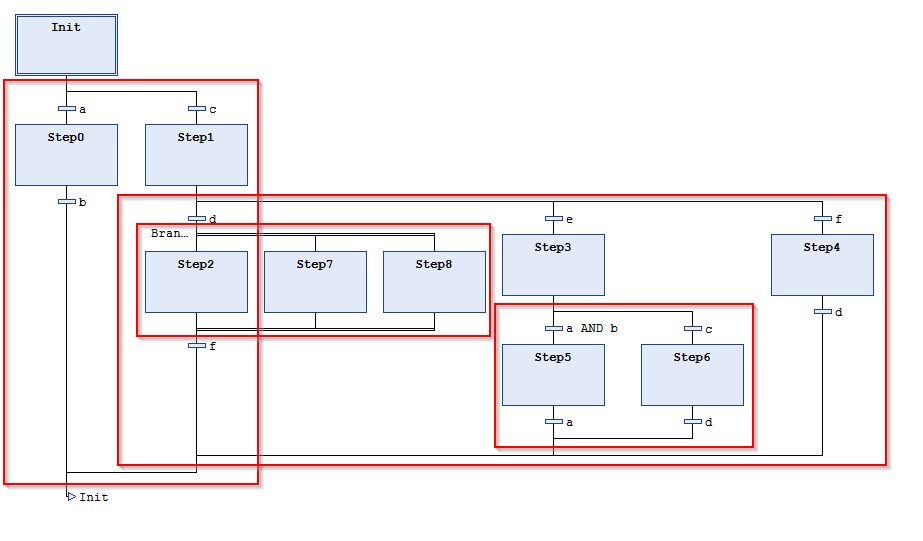 |
The above code snippet in SFC has 4 branches: 3 alternative branches and 1 parallel branch
Metric: Number of SFC steps
Category: Maintainability
Number of steps in a POU in SFC (sequential function chart)
Only the steps are counted which are contained in the POU programmed in SFC. Steps are not counted which are in the implementations of actions or transitions called in POUs.
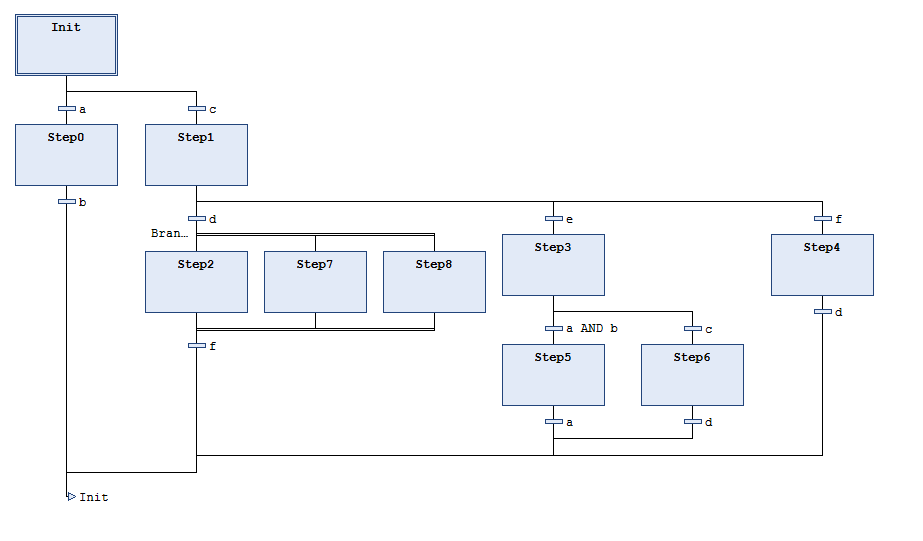 |
The code snippet in SFC has 10 steps.