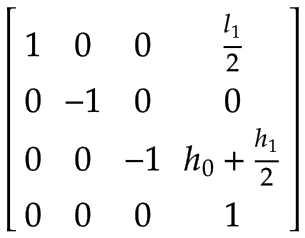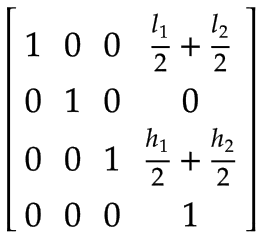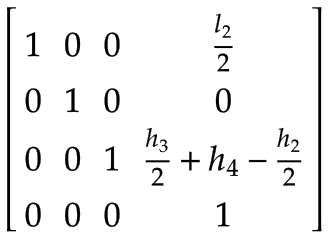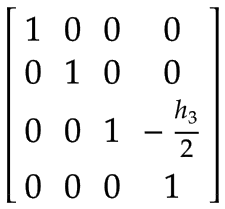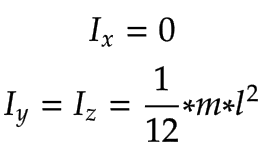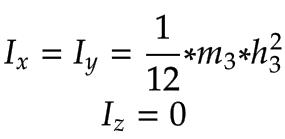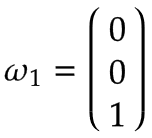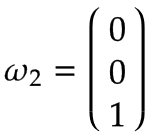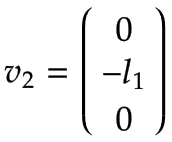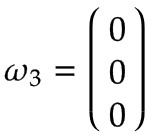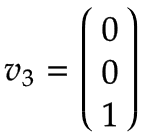Skip to main content

Dynamisches Robotermodell

Sehen Sie hierzu das Beispielprojekt Robotics_DynamicModel.project im Installationsverzeichnis von CODESYS unter ..\CODESYS SoftMotion\Examples.

Um die Achsmomente/-kräfte während einer Bewegung zu begrenzen, ist ein dynamisches Modell erforderlich, das diese Werte aus dem aktuellen Achszustand (Position, Geschwindigkeit und Beschleunigung) berechnet. Dieses Beispiel umfasst die folgenden Teile:

  • Teil 1 zeigt, wie ein bestehendes dynamisches Modell in einer Anwendung verwendet wird und die Ergebnisse einiger Beispielbewegungen

  • Teil 2 zeigt, wie ein dynamisches Modell für einen SCARA-Roboter auf der Grundlage eines Algorithmus erstellt wird, der in dem Buch "Modern Robotics" von K. M. Lynch und F. C. Park vorgestellt wird

Struktur der Applikation

Teil 1: Verwendung eines dynamischen Modells in einer Anwendung

  • Der Code für diesen Teil befindet sich im Ordner TorqueLimitationDemo

  • PLC_PRG ist das Hauptprogramm, das eine Zustandsmaschine enthält, die Testbewegungen auslöst

  • Die Bewegungen können mit dem Trace überwacht werden

Teil 2: Erstellen eines dynamischen Robotermodells

  • Der Code für das dynamische Modell befindet sich im Ordner DynModel

  • DynModel_Scara2_Z ist das dynamische Modell des SCARA-Roboters

  • DynModel_Tests führt alle Tests von Test_DynModel_Scara2_Z aus, um auf häufige Fehler zu prüfen

  • Das dynamische Modell basiert auf einem SCARA-Roboter mit zwei rotatorischen Achsen und einer linearen Z-Achse. Eine Abbildung des Roboters mit den erforderlichen Abmessungen und Koordinatensystemen für das dynamische Modell ist unten dargestellt:

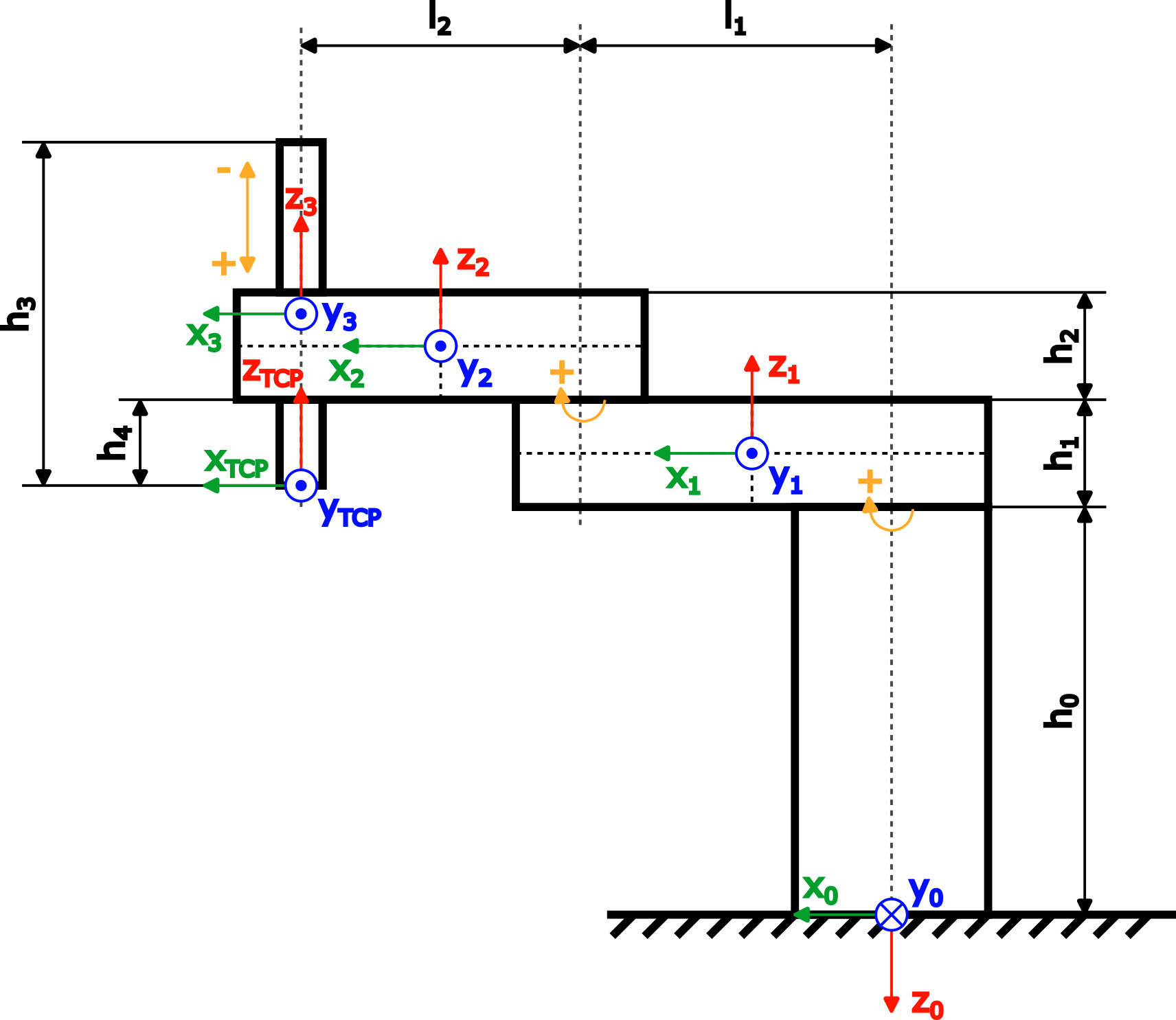
    _sm_img_dynmodel_scara_2_z.png

    Abmessung in der Abbildung

    Entsprechender Variablenname im Beispielprojekt im Funktionsbaustein DynModel_Scara2_Z

    h0

    baseHeight

    h1

    armOneHeight

    h2

    armTwoHeight

    h3

    zAxisLength

    h4

    zAxisOffset

    l1

    armOneLength

    l1

    armTwoLength

Teil 1: Verwendung eines dynamischen Modells in einer Anwendung

Die Verwendung eines dynamischen Modells in einer Anwendung erfordert ein Modell, das die Schnittstelle ISMDynamics der Bibliothek SM3_Dynamics implementiert. Das dynamische Modell aus Teil 2: Erstellen eines dynamischen Robotermodells wird für diese Demonstration verwendet.

Das Modell kann mit SMC_GroupSetDynamics einer Achsengruppe zugewiesen werden. In diesem Schritt muss die Erdbeschleunigung in Bezug auf das MCS angegeben werden. Da der SCARA in diesem Beispiel am Boden montiert ist, zeigt die Erdbeschleunigung in die positive z0-Richtung. Die Erdbeschleunigung muss in Benutzereinheiten u/s² angegeben werden. Da alle Längen in diesem Beispiel in der Benutzereinheit m definiert wurden, muss auch die Erdbeschleunigung in m/s² angegeben werden.

SMC_ChangeDynamicLimits kann verwendet werden, um die Grenzen jeder Achse anzupassen. Bitte beachten Sie, dass die Achsgruppe mit MC_GroupEnable wieder aktiviert werden muss, um die neuen dynamischen Grenzen zu aktivieren.

Wenn dem TCP zusätzliche Massen hinzugefügt werden (beispielsweise ein Werkzeug oder ein Objekt, das vom Roboter aufgenommen wurde), kann SMC_GroupSetLoad verwendet werden, um die Last zu definieren.

Das Programm PLC_PRG enthält alle oben genannten Komponenten und führt zwei Testbewegungen aus:

Bewegung 1

Bewegung 2

Gerade Armbewegung von (a0=0°, a1=0°, a2=0 m) nach (a0=90°, a1=0°, a2=0,02 m):

_sm_img_dynmodel_one.png

Abgewinkelte Armbewegung von (a0=0°, a1=-120°, a2=0 m) nach (a0=90°, a1=-120°, a2=0,02 m):

_sm_img_dynmodel_two.png

Jede Bewegung wird dreimal hintereinander mit den folgenden Randbedingungen ausgeführt:

  • Die Drehmomentgrenze aller Achsen ist unendlich (unbegrenzt).

  • Die Drehmomentgrenze von Arm 2 ist auf einen niedrigeren Wert als das maximal erreichte Drehmoment bei unbegrenzter Bewegung eingestellt. Der Wert wurde willkürlich auf 2 Nm festgelegt.

  • Die Drehmomentgrenze von Arm 2 beträgt immer noch 2 Nm, und zusätzlich wurde eine Last am TCP angebracht (mLoad=3 kg, lLoad=0,2 m):

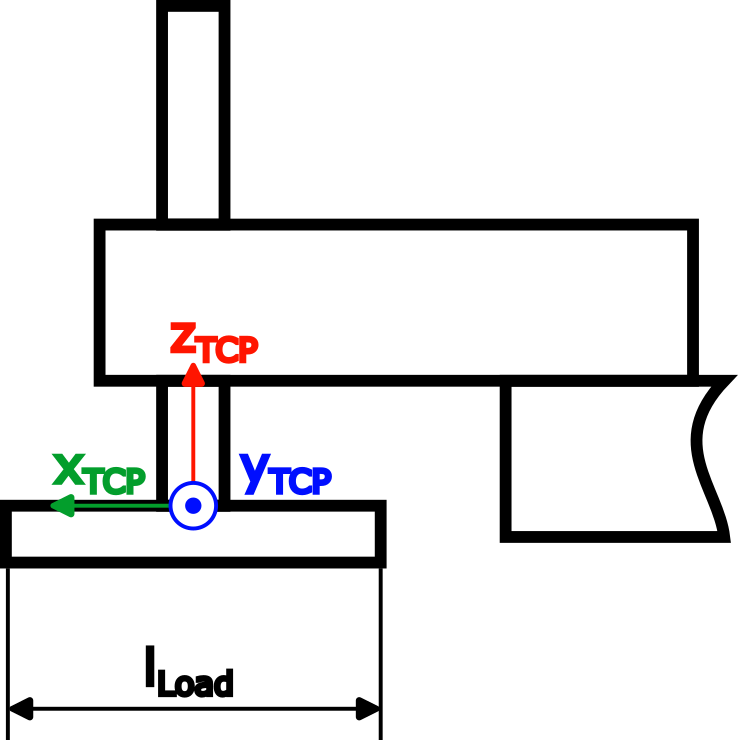_sm_img_robot_with_load.png

Das Massenträgheitsmoment der Last wurde vereinfacht für dünne Stäbe berechnet:

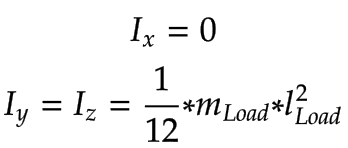_sm_img_load_inertia_tensor.png

Die Bewegungen können im Trace verfolgt werden. Bewegung 1 hat die folgenden Ergebnisse:

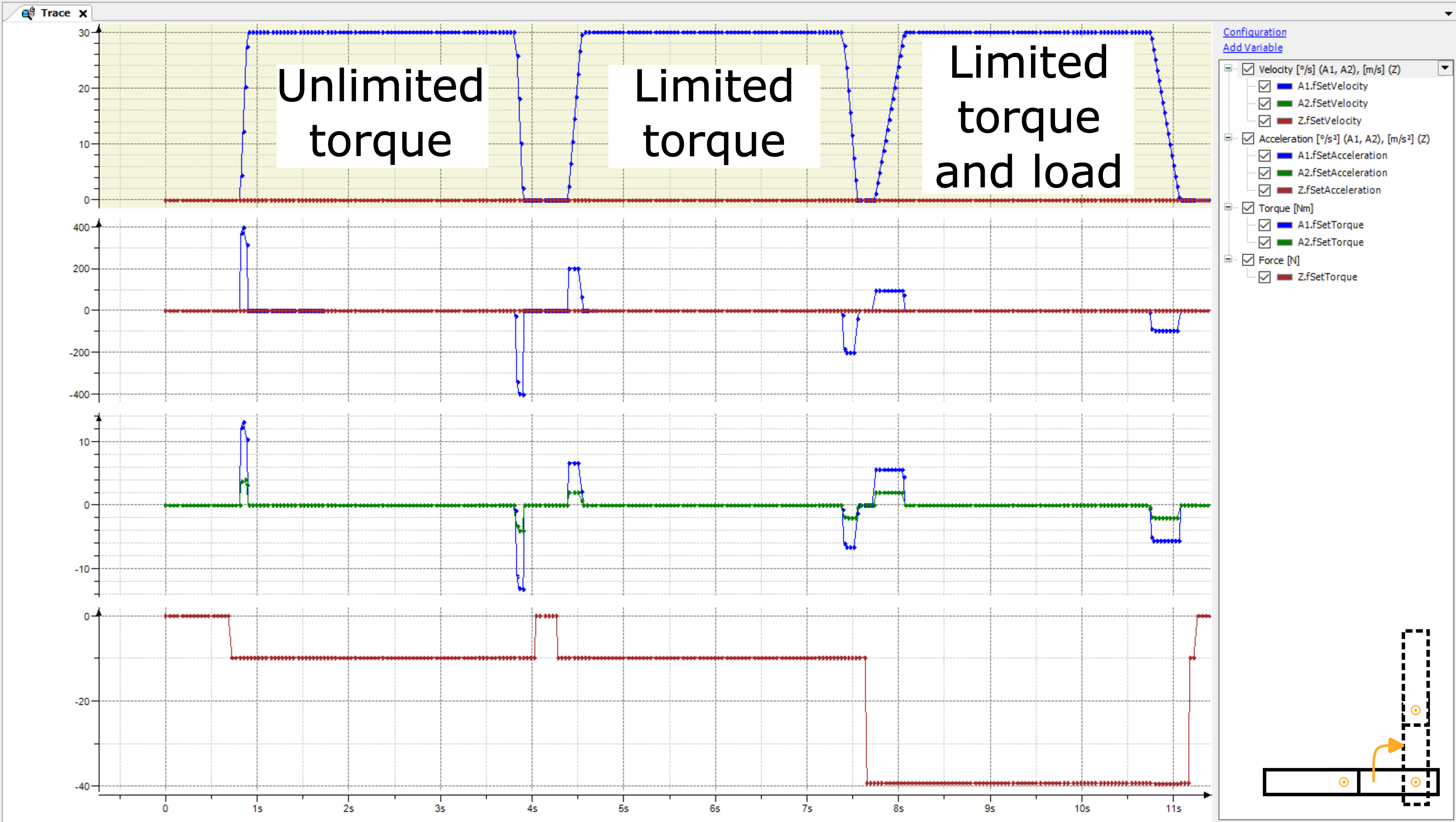
_sm_img_movement_one_results.png

  • Auch wenn sich Arm 2 während der Bewegung 1 nicht bewegt, führt die Beschleunnigung/Verzögerung von Arm 1 zu einem Drehmoment in Arm 2. Das berechnete Drehmoment wird an den Antrieb gesendet und kann den Regelkreis im Reglermodus SMC_velocity oder SMC_position verbessern. Dies wird auch als Drehmoment-Vorsteuerung bezeichnet.

  • Der zweite Durchlauf mit begrenztem Drehmoment zeigt, dass die Drehmomentbegrenzung von Arm 2 zu einer langsameren Bewegung von Arm 1 führt. Und das auch, wenn sich Arm 2 nicht bewegt. Ohne das dynamische Modell müsste die Beschleunigung und Abbremsung von Arm 1 für diese Bewegung manuell reduzieren werden, um eine übermäßige mechanische Belastung von Arm 2 zu vermeiden.

  • Beim dritten Durchlauf mit einer Last, wird die Bewegung von Arm 1 noch langsamer, um die Drehmomentgrenze von Arm 2 nicht zu verletzen.

Die Vorteile der Verwendung eines dynamischen Modells liegen auf der Hand. Um übermäßige mechanische Belastung ohne dynamisches Modell zu verhindern,

  • müssten entweder die dynamischen Grenzen für jede Bewegung in Abhängigkeit vom aktuellen Zustand des Roboters festgelegt werden.

  • müssten die dynamischen Grenzen aller Achsen so verringert werden, dass alle möglichen Bewegungen nicht zu einer übermäßigen mechanischen Belastung einer Achse führen.

Die erste Methode ist eine komplexe Aufgabe und es kann schwierig sein, vernünftige Grenzwerte zu berechnen, während die zweite Methode zu Bewegungen führt, die meistens nicht so schnell wie möglich sind. Diese Nachteile sind bei einem dynamischen Modell nicht mehr vorhanden, da sich der Roboter immer so schnell wie möglich bewegt und dabei die mechanischen Grenzen jeder Achse beachtet.

Diese Vorteile verdeutlichen die Ergebnisse von Bewegung 2:

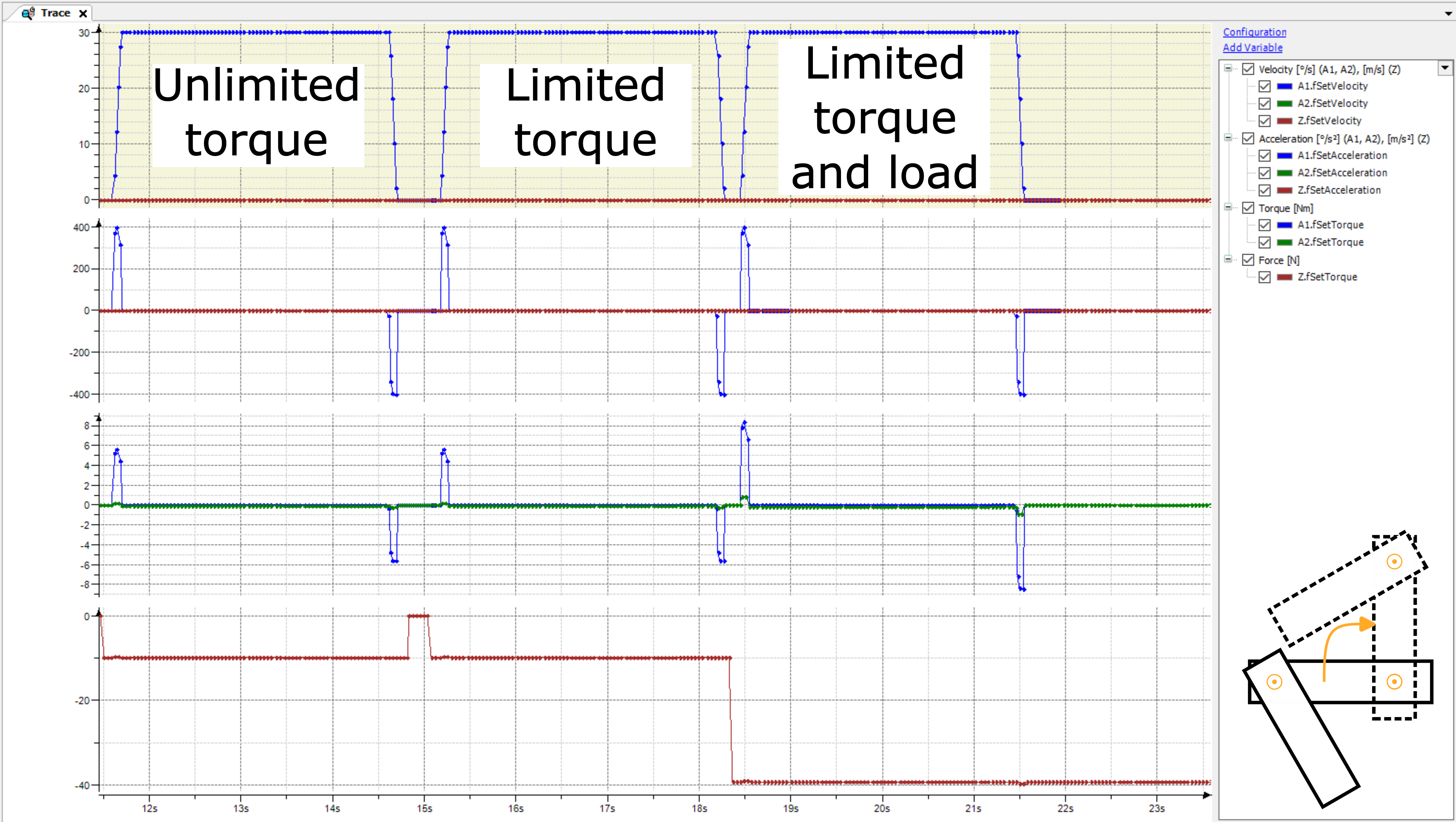
_sm_img_movement_two_results.png

Aufgrund des abgewinkelten Arms 2 ist das resultierende Drehmoment des Arms 2 wesentlich geringer als bei Bewegung 1. Daher werden alle drei Fahrten nie durch das Achsendrehmoment begrenzt. Hätte man auf der Grundlage von Bewegung 1 angepasste dynamische Grenzwerte verwendet (reduzierte Beschleunigung und Abbremsung, um die Drehmomentgrenze von Arm 2 nicht zu verletzen), wäre diese Bewegung langsamer als nötig gewesen.

Teil 2: Erstellen eines dynamischen Robotermodells

Das Modell, das in diesem Beispiel erstellt wird, basiert auf einem Algorithmus für Roboter mit offenen Ketten, der in dem Buch "Modern Robotics" von K. M. Lynch und F. C. Park vorgestellt wird (siehe Kapitel 8 "Dynamics of Open Chains"). Die Erläuterung dieses Algorithmus würde den Rahmen dieses Beispiels sprengen. Stattdessen konzentriert sich das Beispiel darauf, wie die Eingangswerte des Algorithmus definiert werden.

Vereinfachungen

Um dieses Beispiel verständlicher zu machen, wurden einige Vereinfachungen vorgenommen:

  • Die Armlängen l1 und l2 (Abstand zwischen den Drehachsen) werden als ihre jeweilige Gesamtarmlänge verwendet.

  • Der Massenschwerpunkt liegt immer in der geometrischen Mitte eines jeden Glieds.

  • Die räumlichen Massenträgheitsmomente der Arme und der z-Achse werden für dünne Stäbe berechnet.

Anforderungen an das dynamische Modell

Um das dynamische Modell in einer SoftMotion-Anwendung verwenden zu können, muss dieses Modelldie Schnittstelle ISMDynamics der Bibliothek SM3_Dynamics implementieren.

Die Nullposition, die Koordinatensysteme und die positive Drehrichtung des dynamischen Modells können theoretisch vom kinematischen Modell abweichen. Diese Unterschiede müssen jedoch berücksichtigt werden, und zur Vereinfachung des dynamischen Modells wird daher empfohlen, die Definitionen des kinematischen Modells zu verwenden.

Da das dynamische Modell Drehmomentwerte in Nm und Kräfte in N berechnen muss, muss es die Benutzereinheit u für Längen in die SI-Einheit m umrechnen. Der Umrechnungsfaktor kann mit SMC_GroupSetUnits eingestellt werden und ist im Eingang addParams von ISMDynamics.AxesStateToTorque enthalten. Dieses Beispiel verwendet nur m für Längen und kann daher den Umrechnungsfaktor ignorieren.

Spezifizierung der geometrischen und dynamischen Daten des Modells

Die IEC-Implementierung des im Buch "Modern Robotics" von K. M. Lynch und F. C. Park vorgestellten Algorithmus (siehe Kapitel 8 "Dynamics of Open Chains") benötigt die folgenden Eingabewerte:

  • Die Position des Massenschwerpunkts jedes Glieds, wenn sich der Roboter in der Ausgangsposition befindet. Die Position wird im Koordinatensystem des vorherigen Glieds angegeben (das erste Glied wird relativ zum Basiskoordinatensystem angegeben).

  • Die räumliche Massenträgheitsmatrix und die Masse jedes Glieds, angegeben im Frame des jeweiligen Glieds

  • Die Schraubenachse jeder Verbindung, angegeben im Basis-Frame

Positionen des Massenschwerpunkts

Die Frames mit der Position des Massenschwerpunkts jedes Glieds sind:

Glied

Frame

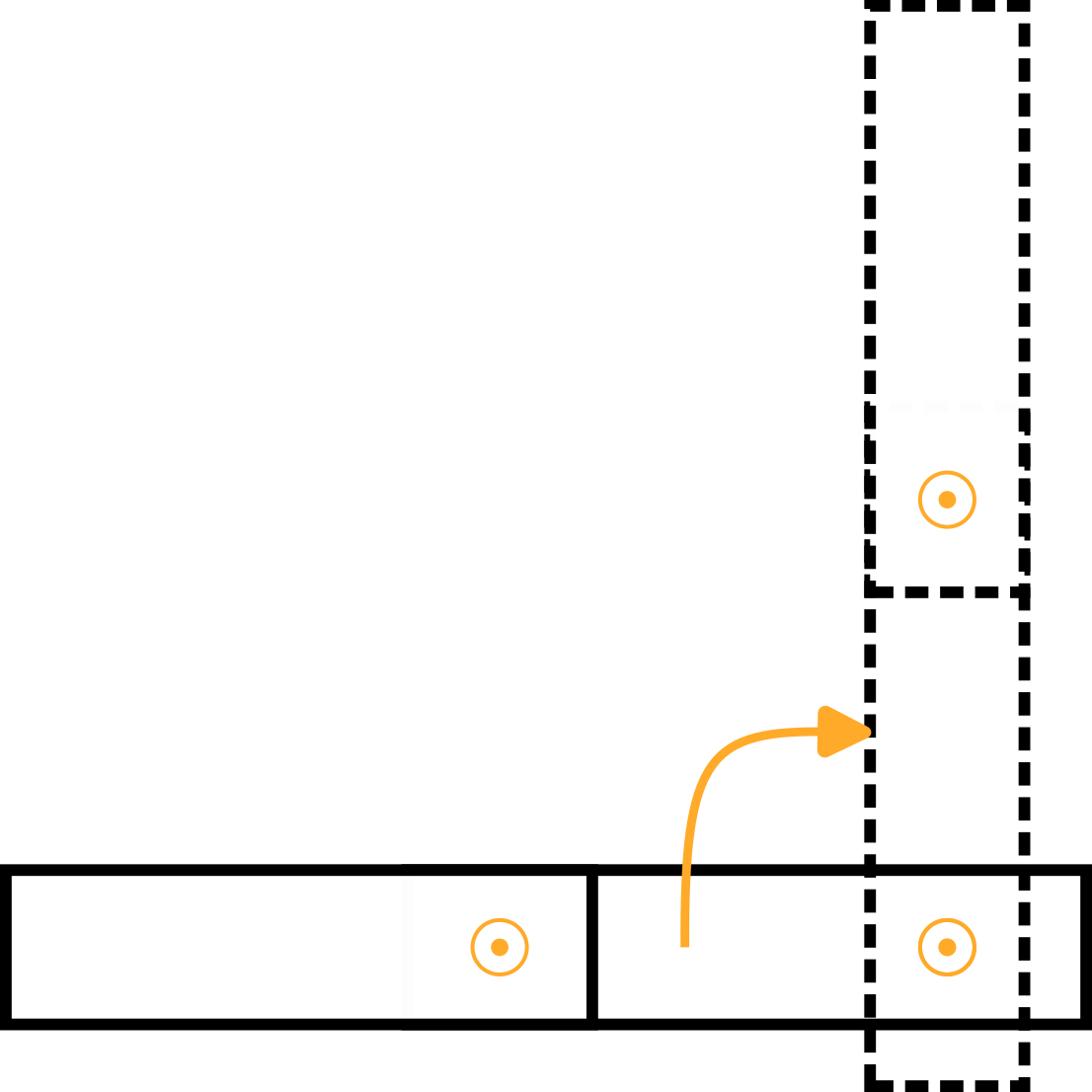
Arm 1

Der Massenschwerpunkt von Arm 1, ausgedrückt im Basiskoordinatensystem x0, y0, z0:

_sm_img_arm1_centerofmass_frame.png

Bitte beachten Sie, dass es eine Drehung um 180° um die x0-Achse gibt.

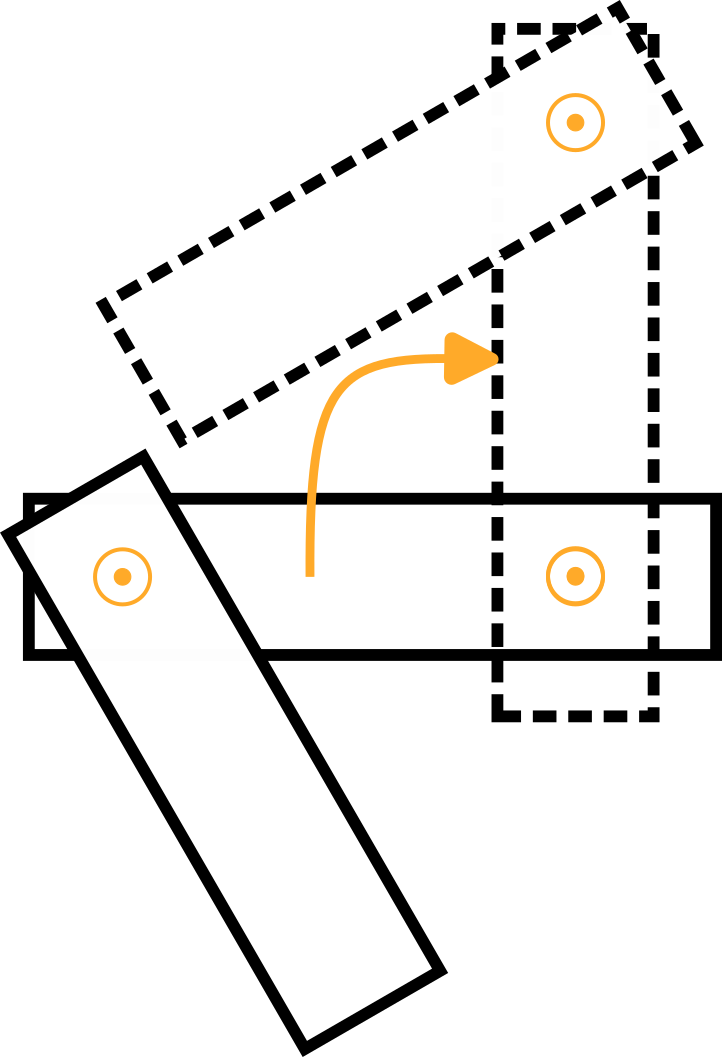
Arm 2

Der Massenschwerpunkt von Arm 2, ausgedrückt im Koordinatensystem von Arm 1:

_sm_img_arm2_centerofmass_frame.png

Z-Achse

Der Massenschwerpunkt der Z-Achse, ausgedrückt im Koordinatensystem von Arm 2:

_sm_img_zaxis_centerofmass_frame.png

Werkzeugmittelpunkt (TCP)

Ein zusätzlicher Frame zur Behandlung einer beliebigen Belastung am TCP (beispielsweise durch ein Werkzeug, ein Objekt oder eine Kombination aus beidem), ausgedrückt im Koordinatensystem der Z-Achse:

_sm_img_externalforce_centerofmass_frame.png

Räumliche Massenträgheitsmomente

Die Trägheitsmomente müssen in dem Frame des jeweiligen Glieds angegeben werden. Da der Frame im Massenschwerpunkt liegt, kann das räumliche Massenträgheitsmoment mithilfe einer 3x3-Matrix und der Masse dargestellt werden.

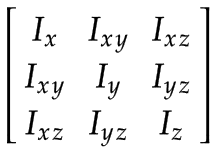_sm_img_general_inertia_tensor.png

Durch die Vereinfachung, dünne Stäbe zu verwenden, berechnen sich die Komponenten der Matrix folgendermaßen:

Glied

Komponenten der Trägheitsmatrix

Arm 1, Arm 2

Arm 1 und 2 mit ihrer jeweiligen Masse m1, m2 und Länge l1, l2:

_sm_img_arm1_arm2_inertiatensor.png

Z-Achse

_sm_img_zaxis_inertiatensor.png

Schraubenachsen

Die Schraubenachsen aller Gelenke müssen in Bezug auf das Basiskoordinatensystem x0, y0, z0 angegeben werden.

Glied

Schraubenachse

Arm 1

Stellen Sie sich einen Drehtisch vor, der sich um das Gelenk 1 in positiver Richtung mit einer Winkelgeschwindigkeit von 1 rad/s dreht.

Im Basiskoordinatensystem ausgedrückt, handelt es sich nach der Rechten-Hand-Regel um eine positive Drehung um die z0-Achse:

_sm_img_arm1_screwaxis_angularvelocity.png

Da die Drehachse von Arm 1 mit dem Mittelpunkt des Basiskoordinatensystems übereinstimmt, ist die lineare Geschwindigkeit gleich Null: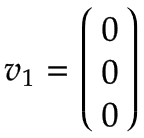

_sm_arm1_screwaxis_linearvelocity.png

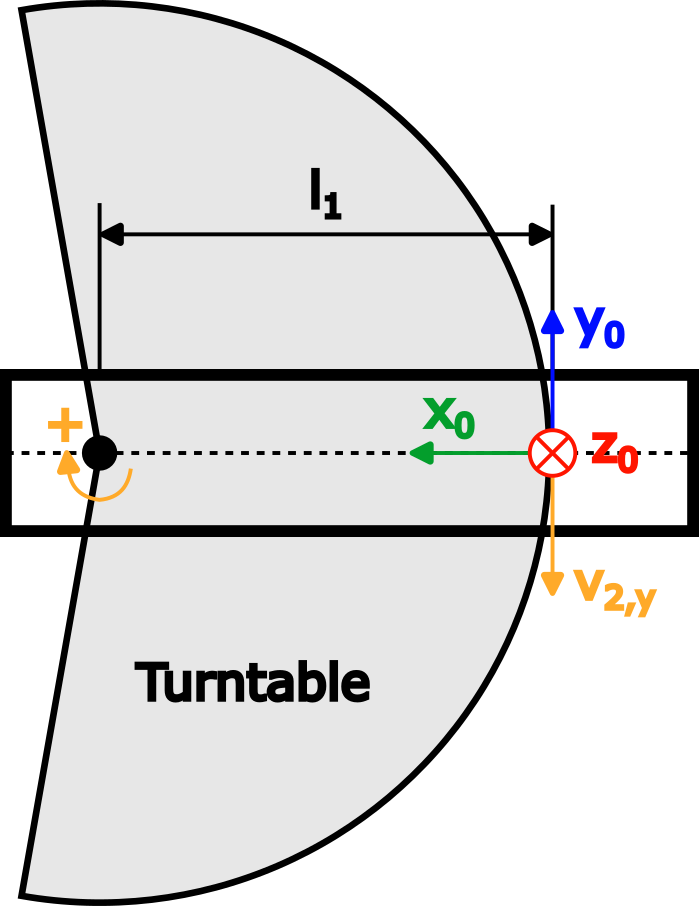
Arm 2

Stellen Sie sich wiederum einen Drehtisch vor, der sich um das Gelenk 2 in positiver Richtung mit einer Winkelgeschwindigkeit von 1 rad/s dreht. Dieser Fall ist nachfolgend als Draufsicht von Arm 1 dargestellt:

_sm_img_arm2_screwaxis.png

Wie für Arm 1, beträgt die Winkelgeschwindigkeit:

_sm_img_arm2_screwaxis_angularvelocity.png

Die Abbildung zeigt die resultierende lineare Geschwindigkeit v2,y, die in negative y0-Richtung zeigt und gleich v2,y=-ω2,z * l1 ist.

_sm_img_arm2_screwaxis_linearvelocity.png

Z-Achse

Die Z-Achse ist eine lineare Achse, für die die folgenden Regeln gelten:

  • Der Winkelgeschwindigkeitsvektor ω ist Null.

  • Der lineare Geschwindigkeitsvektor ist ein Einheitsvektor in Richtung der positiven Translation.

Daraus ergeben sich die folgenden Vektoren, ausgedrückt im Basiskoordinatensystem x0, y0, z0:

_sm_img_zaxis_screwaxis_angularvelocity.png
_sm_img_zaxis_screwaxis_linearvelocity.png

Tests

Das dynamische Modell kann nun getestet werden, da alle Modellparameter definiert sind. Dieser Abschnitt enthält einige grundlegende Tests des Modells.

Kontrolle der Schraubenachsen

Eine Schraubenachse S mit der Winkelgeschwindigkeit ω und der linearen Geschwindigkeit v kann als ein Element von se(3) ausgedrückt werden:

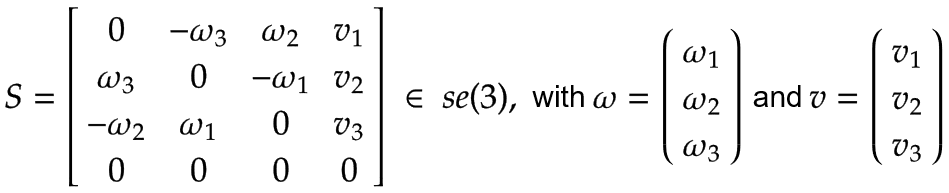_sm_img_screwaxis_se3.png

Eine Vorwärtstransformation T kann mit den Schraubenachsen S, einem Endeffektor-Frame M für die Nullposition des Roboters und dem Gelenkwinkel θ jedes Gelenks ausgeführt werden:

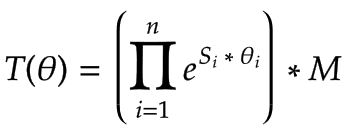_sm_img_screwaxis_forwardtransformation.png

Das Beispielprojekt enthält bereits eine Funktion, die diese Gleichung löst (siehe SMC_OpenChainKinematics_SolveForward). Für weitere Details siehe das Buch "Modern Robotics" von K. M. Lynch und F. C. Park.

Wenn die Vorwärtstransformation mit bekannten Achswerten ausführt wird, kann überprüft werden, ob die Transformation zum erwarteten Ergebnis führt.

Überprüfung der Drehmomente im Stillstand

Um die grundsätzliche Berechnung des Drehmoments zu überprüfen, können manuell Drehmomente für bestimmte Achspositionen im Stillstand berechnet und diese mit dem Modell verglichen werden. Da der SCARA-Roboter in diesem Beispiel auf dem Boden montiert ist, führen alle Achsenpositionen im Stillstand zu den gleichen Drehmomenten oder Kräften der Antriebe:

Gelenk

Resultierendes Drehmoment/Kraft

Arm 1

Da es sich bei Arm 1 um eine Drehachse handelt, ist das Ergebnis ein Drehmoment: M1=0 Nm.

Arm 2

Da es sich bei Arm 2 um eine Drehachse handelt, ist das Ergebnis ein Drehmoment: M2=0 Nm.

Z-Achse

Da die Z-Achse eine prismatische Achse ist, ergibt sich daraus eine Kraft: F3=m3*g N mit der Gravitationsbeschleunigung g.

In diesem Abschnitt: