Definition einer SoftMotion-Kurvenscheibe
Eine Kurvenscheibe beschreibt die funktionale Abhängigkeit eines Antriebs (Slave) von einem anderen Antrieb (Master). Die Beziehung wird beschrieben durch eine stetige Funktion (oder Abbildung), die einen definierten Bereich an Masterwerten auf Slavewerte abbildet. Noch genauer: Nach Unterteilen der Masterachse in geeignete Abschnitte kann der Graph dieser Funktion auf jedem dieser Intervalle entweder durch eine Gerade oder aber durch ein Polynom 5. Grades dargestellt werden.
Die Masterwerte sind auf der horizontalen, die Slavewerte auf der vertikalen Achse im Graphen einer Kurvenscheibe aufgetragen.
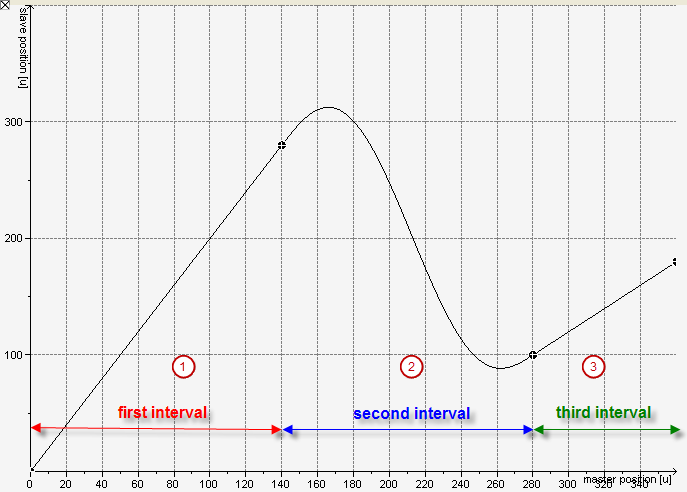
Im Beispiel liegen die Masterwerte zwischen 0 und 360. Dieser Bereich ist in drei Intervalle unterteilt:
(1) erstes Intervall: [0, 140]
(2) zweites Intervall: [140, 280]
(3) drittes Intervall: [280, 360]
Auf dem ersten und dritten Intervall ist die Funktion (Abbildung) linear, ihr Graph entsprechend eine Gerade. Demzufolge ist ihre erste Ableitung (Steigung) konstant, alle höheren Ableitungen sind 0.
Auf dem mittleren Intervall wird die Abbildung durch ein Polynom fünften Grades beschrieben. Somit ist ihre erste Ableitung ein Polynom vierten Grades, ihre zweite Ableitung (die Krümmung) ein Polynom dritten Grades, ihre dritte Ableitung ein Polynom zweiten Grades (usw.).
Wenn die Funktion die Bewegung des Slaves in Abhängigkeit von der Position des Masters beschreibt, so entspricht ihre erste Ableitung gerade der Geschwindigkeit des Slaves, die zweite Ableitung seiner Beschleunigung.
Behält man diese physikalische Interpretation im Hinterkopf, so wird offensichtlich, dass die Abbildung stetig sein muss. Das bedeutet, dass ihr Graph keine Sprünge aufweisen darf. Insbesondere muss die Stetigkeit auch an jedem Punkt erfüllt sein, an dem zwei Intervalle zusammentreffen. Des Weiteren wird die Stetigkeit im Allgemeinen auch von der ersten und zweiten Ableitung gefordert. (In der Tat bestimmen diese drei Stetigkeitsforderungen an Anfangs- und Endpunkt eines Intervalls gerade die Koeffizienten des zwischen zwei Geradenstücken eingefügten Polynoms fünften Grades.
Außerdem dürfen Sie an beliebigen Stellen Nocken, das heißt binäre Schalter, zur Kurvenscheibe hinzufügen. Damit können Sie Kurvenscheibentabellen anlegen, die nur Nocken enthalten. Die Slaveposition wird dann über den gesamten Masterwertebereich auf 0 gesetzt.